Une tour de refroidissement est un échangeur d'un type particulier qui permet de rejeter de la chaleur dans l'air environnant sous forme à la fois de chaleur sensible et de chaleur latente du fait de l'augmentation de son humidité.

En opérant de la sorte, il est possible de refroidir un fluide jusqu'à une température supérieure de quelques degrés à la température humide de l'air ambiant (et donc éventuellement inférieure à sa température sèche), ceci au prix d'une quantité d'eau consommée de l'ordre de 5 % de celle que demanderait un refroidissement à eau. Tant sur le plan économique qu'environnemental, les tours de refroidissement sont des systèmes très intéressants, notamment en climat chaud et sec.

On distingue deux grandes catégories de tours de refroidissement, celles dites à contact direct ou à cycle ouvert, et celles dites à contact indirect ou à cycle fermé.

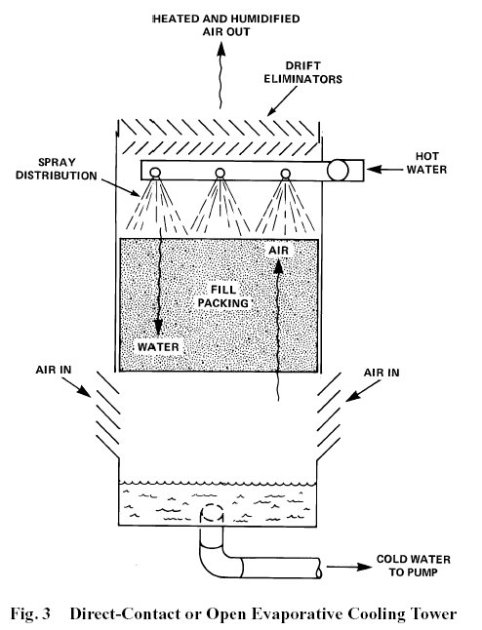
Dans une tour à contact direct, l'eau chaude à refroidir est mise en contact avec l'air ambiant, soit par pulvérisation en fines gouttelettes, soit par ruissellement le long de surfaces d'écoulement. Les deux fluides étant en contact, de la chaleur est échangée par convection, et une partie de l'eau se vaporise, en augmentant ainsi l'humidité de l'air. Si celui-ci n'est pas saturé, il commence par se refroidir de manière quasiment adiabatique, avant de s'échauffer le long de la courbe de saturation. L'eau peut donc ressortir à une température inférieure à celle de l'air ambiant.

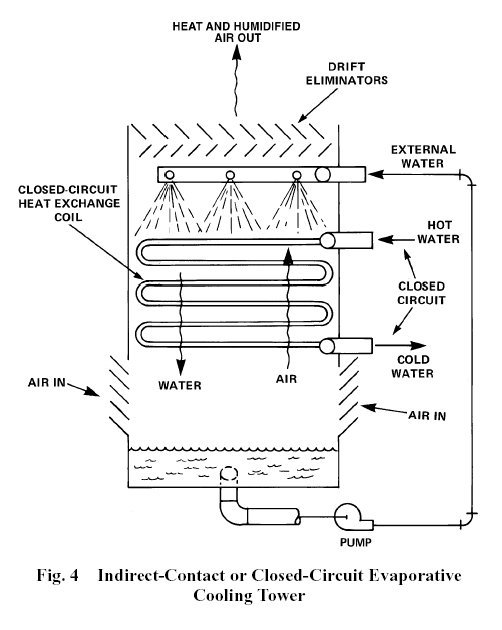
Une tour à contact indirect met en jeu deux circuits, dits externe et interne. Dans ce dernier, le fluide à refroidir, qui peut être quelconque, reste confiné dans un faisceau de tubes autour desquels ruisselle l'eau de refroidissement du circuit externe, qui se réchauffe à son contact, puis se refroidit par échange avec l'air ambiant selon le même mécanisme que dans une tour à contact direct.

Du fait de l'évaporation d'une partie de l'eau, la concentration des sels dissous et celle des impuretés, notamment biologiques, est amenée à augmenter. On doit donc d'une part procéder à des purges de déconcentration, et d'autre part veiller à éviter tout risque de propagation de légionellose.

La modélisation théorique des tours de refroidissement est assez complexe compte tenu de la multiplicité des transferts qui y prennent place. On trouvera une présentation d'un tel modèle dans la fiche guide de TD n° 6 sur les tours de refroidissement.

Les hypothèses généralement faites, dues à Merkel, sont les suivantes :

• l'air sortant de la tour est quasiment saturé

• le film interstitiel est de l'air saturé d'humidité, à la température de l'eau

• le nombre de Lewis est égal à 1

• la résistance thermique côté liquide est négligée devant celle côté air

Elles permettent d'aboutir à un modèle dans lequel la principale caractéristique de la tour est un Nombre d'Unités de Transfert NUTm, résultat de l'intégration de l'équation suivante.

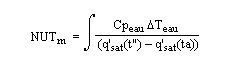
Il s'agit d'un indicateur représentatif de la difficulté qu'il y a à effectuer le transfert thermique dans la tour de refroidissement. Incorporant des phénomènes couplés d'échange d'énergie et de masse complexes, et dépendant de la technologie mise en œuvre, il n'est pas possible d'en donner une expression simple.

On appelle " approche" (en anglais " approach") le pincement^[1] de la tour, c'est-à-dire l'écart entre la température de sortie de l'eau et la température humide de l'air ambiant et " refroidissement" (en anglais " range") la valeur de la variation de température de l'eau.

  NUT est généralement fonction de quatre variables :

• le rapport du débit massique d'eau au débit massique d'air

• la température humide de l'air à l'entrée de la tour

• soit les deux températures de l'eau Tee et Tes

• soit le refroidissement (Tee - Tes) et l'approche (Tes - T'ae).

De nombreux auteurs se sont intéressés à la modélisation des tours de refroidissement, et ont cherché des expressions de NUT qui soient à la fois faciles à calculer et en accord avec les résultats expérimentaux. Étant donné qu'il s'agit avant tout d'un indicateur de performance, il n'est pas en soi rédhibitoire qu'il existe une part d'arbitraire dans sa définition, dans la mesure cependant où les conventions retenues sont bien précisées.

L'expérience montre que, lorsque l'on modifie les quatre variables d'entrée d'une tour de refroidissement donnée, NUTm prend des valeurs diverses, qui suivent une loi de comportement du type suivant, n et m ayant des valeurs négatives comprises entre -1,1 et -0,35, et C étant compris entre 1 et 2,5 environ. C et n ou m sont appelés les coefficients de la tour.

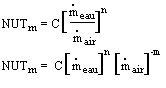
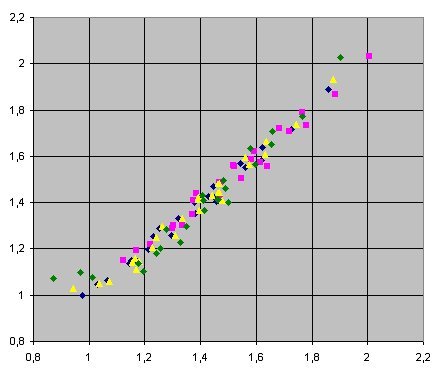
Correspondance entre NUTm constructeur et corrélation

Cette figure montre la très bonne correspondance qui existe entre les valeurs de NUTm calculées pour le même modèle de tour de refroidissement (F1221 de la société Marley ) avec quatre motorisations de ventilateur différentes (40, 50, 60 et 70 hp).

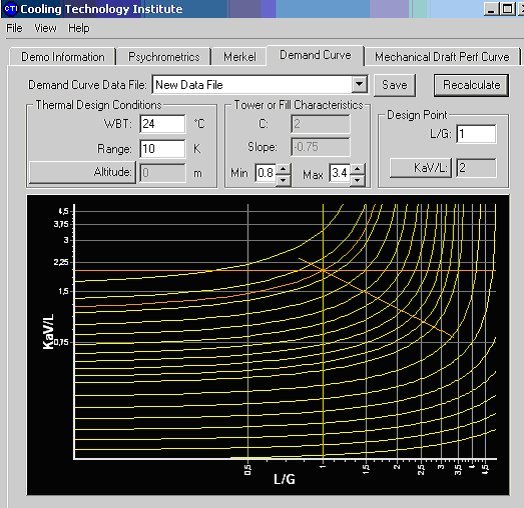
Le Cooling Technology Institute a développé un outil appelé Toolkit, dont une version de démonstration est librement téléchargeable, qui permet d'intégrer l'équation différentielle donnant NUTm. Une comparaison avec nos résultats conduit à un écart très faible, inférieur à 2 %, vraisemblablement dû à une différence dans la modélisation des propriétés des fluides.

Avec les unités anglo-saxonnes, NUTm s'exprime sous la forme :

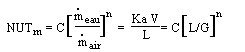
Les caractéristique des tours de refroidissement obtenues ont l'aspect donné ci-dessus, en coordonnées bi-logarithmiques. En abscisse apparaît le rapport L/G du débit massique d'eau sur celui d'air, et en ordonnée NUTm. La valeur de design est affichée en orange, ainsi qu'une courbe représentant le modèle de comportement.

Cet abaque peut ainsi être utilisé pour caractériser une tour donnée :

• la valeur de NUTm pour les conditions de design est calculée

• la droite de pente n et de constante C est tracée et ajustée sur le point de design

• pour des conditions d'utilisation autres, déterminées par la donnée des débits des fluides, l'abaque permet de trouver, à l'abscisse L/G et sur la droite caractéristique de la tour, les nouvelles valeurs de NUTm et de l'approche, ce qui fixe la température de sortie d'eau et donc la puissance. La température de sortie d'air s'en déduit. Pour un autre refroidissement ou une autre température humide de l'air ambiant, il est possible de recalculer un autre abaque. Connaissant les valeurs du couple (NUTm, L/G) à partir de l'abaque initial, on obtient la nouvelle approche.

Étant donné que c'est la variation d'enthalpie de l'air humide saturé qui caractérise le mieux le comportement thermodynamique de l'air, un certain nombre d'auteurs considèrent que tout se passe comme si l'eau échangeait avec un fluide fictif dont la chaleur massique à pression constante serait égale à la capacité calorifique moyenne de l'air humide saturé, mais il est aussi possible de l'exprimer en fonction de la chaleur massique de l'air sec.

Il faut donc bien prendre garde aux conventions retenues pour ne pas se tromper dans les calculs. L'essentiel est d'être parfaitement homogène dans l'ensemble de l'approche retenue : il faut bien veiller à ce que les conventions utilisées pour l'identification des valeurs de C et n à partir des valeurs expérimentales soient les mêmes que celles retenues pour calculer e et NUT.

Le lecteur intéressé se référera aux documents cités en référence pour plus de détails.

Il nous semble cependant nécessaire de mettre en garde le lecteur : nous avons essayé d'implémenter cette approche sur les quelques données soit expérimentales soit fournies par les constructeurs que nous avons pu nous procurer, et nous nous sommes rendus compte qu'autant, appliquées à NUTm, les corrélations du type Merkel conduisent à des reconstitutions précises avec des valeurs de n et m proches de celles que nous avons indiquées, autant elles peuvent être différentes lorsque l'on a recours à une approche (epsilon, NUT) analogue à celles des échangeurs de chaleur secs. Nous recommandons donc la plus grande prudence lors de l'utilisation de cette analogie, et pensons qu'il est préférable d'appliquer le modèle de Merkel qui a fait ses preuves et est utilisé par la profession. Les calculs sont à peine plus complexes, et peuvent être faits avec des petits programmes ou macros Excel.

Dans ce portail, les principales ressources concernant les tours de refroidissement sont les suivantes :

• un modèle de tour à contact direct

• un modèle de tour à contact indirect

• une fiche-guide de TD permettant d'étudier le couplage d'une tour de refroidissement à une machine de réfrigération

D.R. BAKER, H.A. SHRYOCK. 1961. A comprehensive approach to the analysis of cooling tower performance. ASME Transactions, Journal of Heat Transfer (August), 339.

J.E. BRAUN, S.A. KLEIN, J.W. MITCHELL, "Effectiveness Models for Cooling Towers and Cooling Coils", ASHRAE Transactions, Vol. 92, Part 2, p. 164-174, 1989 ASHRAE Handbook 2000, "Cooling Towers", chapter 36

ASHRAE Handbook 2000, "Cooling Towers", chapter 36

F. KREITH, "The CRC Handbook of Thermal Engineering", CRC Press Springer, 3 "Cooling Towers", by A.F. Mills, Chapter 4.9, 1999