Maintenant que nous avons introduit le premier principe, établi son expression enthalpique et montré combien simplement il s'applique aux quatre évolutions élémentaires que subissent les fluides dans les machines qui nous intéressent, nous pouvons discuter des avantages et inconvénients des différentes variables d'état que l'on peut envisager utiliser.

Nous avons vu qu'il existe plusieurs jeux de variables d'état pouvant servir à caractériser un système thermodynamique. Les plus « naturelles » sont la température, la pression et le volume, mais d'une part il en existe d'autres, comme l'enthalpie que nous venons de définir, et d'autre part elles ne sont pas pleinement satisfaisantes compte tenu des nos objectifs, comme nous allons le montrer.

La pression P est fondamentale, à la fois parce qu'elle intervient directement dans les contraintes mécaniques auxquelles sont soumis les composants, et parce que, comme nous l'avons vu, l'évolution de référence pour les échauffements et refroidissements de fluide est l'isobare.

La température T est elle aussi essentielle, mais, à la différence de la précédente, l'isotherme ne correspond à aucune des évolutions qui nous intéressent.

Par ailleurs, le couple (P, T) ne suffit pas à représenter l'évolution subie par un fluide lorsqu'il change d'état, les deux variables étant liées par la loi de pression ou température saturante : il manque le titre en vapeur x.

Le volume v n'intervient que très peu dans les analyses qui nous intéressent, même en système fermé^[1], car l'existence de parois mobiles fait que le volume change. En fait, son principal intérêt pratique est de permettre le dimensionnement des sections de passage.

L'enthalpie h est une variable fondamentale elle aussi, car elle est directement liée aux échanges d'énergie qui prennent place dans les machines. Pour les gaz parfaits, c'est une fonction affine de la température, qui s'en déduit donc très facilement.

Pour les fluides réels, dans la zone d'équilibre liquide-vapeur, elle fournit de surcroît l'information sur le titre. Enfin, rappelons que l'isenthalpe est l'évolution de référence d'une détente sans travail.

Pour nos besoins actuels, dans le cadre de cette présentation pédagogique allégée, ces analyses suffisent pour nous permettre de conclure que le couple (P, h) constitue un jeu de variables d'état particulièrement intéressant. Nous en verrons les implications lorsque nous chercherons à représenter graphiquement les cycles des machines que nous étudions, c'est-à-dire leurs évolutions dans des diagrammes thermodynamiques.

L'analyse des transformations subies par les fluides lors des compressions et détentes avec travail nous a montré que l'évolution de référence est l'adiabatique réversible, dont nous avons indiqué qu'elle suit pour un gaz parfait la loi loi 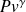= Cste.

Signalons en passant, mais sans insister compte tenu de notre souci de simplicité, que cette loi est celle de l'isentropique. L'entropie s est elle aussi une fonction d'état^[2] très utilisée en thermodynamique, notamment parce que l'isentropique est l'évolution de référence en matière de compression et détente.