10 Diagrammes thermodynamiques
Les systèmes thermodynamiques auxquels nous nous intéressons peuvent être caractérisés par la donnée de deux variables d'état : on dit qu'ils sont bivariants. Cela signifie que leurs propriétés thermodynamiques peuvent être représentées graphiquement dans un plan, sous forme de diagramme thermodynamique.
En mettant en évidence les évolutions de référence des transformations subies par les fluides et en permettant de les calculer, au moins de manière approximative, les diagrammes font partie des outils de base du thermodynamicien. Leur intérêt est double :
permettre de représenter graphiquement les cycles ;
faciliter l'estimation de l'état thermodynamique des différents points du cycle.
Du fait des possibilités offertes par les progiciels de calcul des propriétés des fluides qui sont de plus en plus répandus, le second intérêt a tendance à diminuer tandis que le premier conserve toute son actualité. Visualiser sur un diagramme un cycle calculé à l'aide d'un outil informatisé permet notamment de s'assurer qu'il ne comporte pas de point aberrant dû à une erreur lors de l'entrée des données...
Un diagramme se présente sous forme d'un graphique plan comportant le tracé d'un certain nombre de courbes remarquables, notamment des familles d'isovaleurs des fonctions d'état.
10.1 Différents types de diagrammes
Sur le plan pratique, les principales transformations que l'on rencontre dans les processus industriels mettant en jeu des fluides purs sont, comme nous l'avons vu, des compressions, des détentes, des échanges de chaleur et des laminages.
Il est clair que la température T, la pression P et le titre en vapeur x sont des variables d'état dont la connaissance est nécessaire pour l'étude de ces processus et la conception des équipements.
Les remarques précédentes montrent que l'enthalpie h est aussi très importante. Enfin, la connaissance du volume massique v est nécessaire pour dimensionner les conduits, puisque c'est elle qui permet de passer du débit-masse au débit-volume.
En conclusion, les grandeurs les plus intéressantes sur le plan pratique sont T, P, h, et des informations complémentaires sur x et v peuvent être nécessaires. C'est donc parmi les trois premières que sont choisies les abscisses et les ordonnées des diagrammes que nous pouvons considérer (rappelons que nous excluons ici l'entropie).
Le couple (T, h) est rarement retenu, car les isobares et les adiabatiques réversibles y sont représentées par des courbes présentant des points d'inflexion qui en rendent l'usage délicat. De plus, les variations de T et h sont proportionnelles lorsque le fluide suit la loi des gaz idéaux.
Sauf pour les gaz permanents, c'est-à-dire dont l'état est très éloigné de leurs conditions de saturation, le couple (T, P) est insuffisant, car T et P sont liés par la loi de vapeur saturante dans la zone d'équilibre liquide-vapeur. Il serait en revanche tout à fait utilisable pour représenter le cycle de la turbine à gaz.
Le couple (P, h) est de plus en plus employé, généralement avec une échelle logarithmique pour les pressions. Il correspond au diagramme dit « des frigoristes » parce que ce sont eux qui en ont généralisé l'usage, et sera étudié plus loin.
Enfin, le couple (P, v), diagramme de Clapeyron, présente un intérêt pédagogique certain, surtout pour l'étude des transformations en système fermé[1]. Son inconvénient principal est sa faible lisibilité, la zone des vapeurs étant réduite et les fonctions énergétiques n'apparaissant pas directement.
En conclusion, pour cette présentation pédagogique allégée ne faisant pas appel à l'entropie, le couple (P,h) apparaît bien adapté.
10.2 Diagramme (h, ln(P)), dit des frigoristes
Dans le diagramme dit des frigoristes (figure ci-dessous), on porte en abscisse l'enthalpie, et en ordonnée la pression, le plus souvent selon une échelle logarithmique.
Son sommet correspond au point critique, la partie gauche, ascendante, représente l'ébullition commençante (courbe de bulle), et sa partie droite, descendante, la vapeur saturée (courbe de rosée). Sous cette courbe se trouve le domaine de l'équilibre diphasique liquide-vapeur, et, dans le reste du plan, celui du fluide simple.
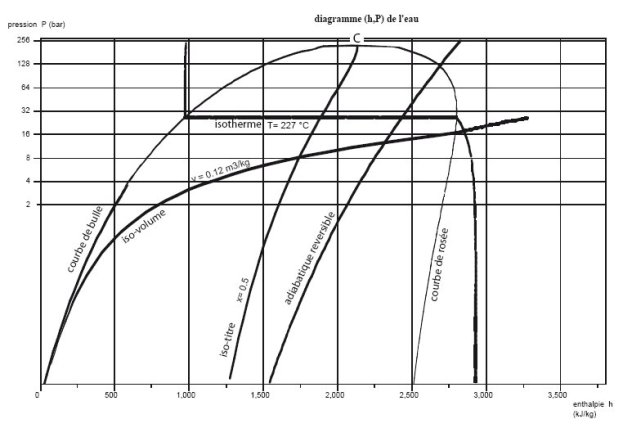
Pour que ce diagramme soit utilisable, on l'équipe avec les adiabatiques réversibles, les isothermes, les isovolumes, et, dans la zone mixte, les courbes d'iso-titre.
Dans la zone "liquide", à gauche du diagramme, les isothermes ont une pente négative très forte : la compression d'un liquide met en jeu un travail très faible.
Dans le domaine diphasique, la pression et la température sont liées par la loi de pression saturante, et les isothermes sont horizontales. L'enthalpie croît énormément, correspondant à la chaleur latente de vaporisation qu'il faut fournir au fluide.
Dans la zone située à droite de la courbe de vaporisation, les isothermes sont des courbes descendantes, qui se rapprochent de verticales pour les valeurs des faibles pressions. En effet, le comportement de la vapeur se rapproche alors de celui d'un gaz idéal, dont l'enthalpie ne dépend que de la température.
Un échauffement ou un refroidissement (isobare) se traduit dans ce diagramme par un segment horizontal, une détente sans travail (isenthalpique) par un segment vertical.
Une adiabatique réversible est une courbe ascendante dont la pente est égale à l'inverse du volume massique. Elles sont donc beaucoup moins inclinées dans la zone vapeur que dans la zone liquide.
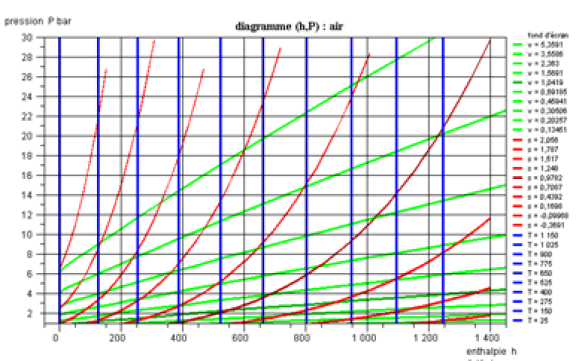
Diagramme (h, ln(P)) des gaz idéaux
Les diagrammes (h, ln(P)) des gaz idéaux sont beaucoup moins répandus que ceux des vapeurs condensables, car généralement, les cycles thermodynamiques des gaz idéaux sont représentés dans le diagramme entropique, auquel nous avons décidé de ne pas faire appel dans cette approche allégée.
Toutefois, même s'ils sont peu usités, ils sont très faciles à utiliser et très clairs.
Dans le diagramme de la figure ci-dessous qui correspond à l'air, assimilable à un gaz idéal, les isothermes sont verticales, les isovolumes et les adiabatiques réversibles, plus pentues étant des courbes à concavité vers le bas.
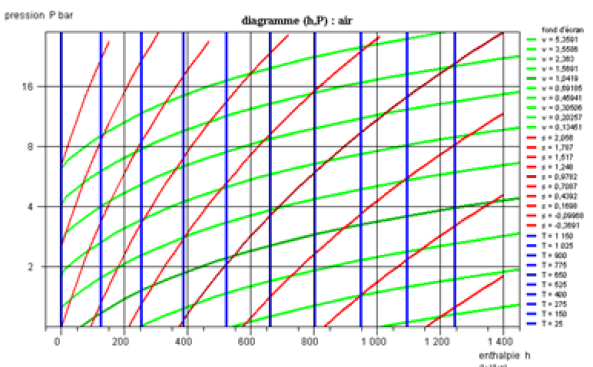
Si on trace le diagramme en coordonnées non logarithmiques (figure ci-dessous), les isovolumes sont des droites, et la concavité des adiabatiques réversibles est orientée vers le haut.