4 Echanges d'énergie entre un système thermodynamique et l'environnement
Il est fondamental de bien noter que les systèmes thermodynamiques mis en jeu dans les composants qui nous intéressent n'échangent de l'énergie avec l'environnement que sous deux formes bien distinctes uniquement :
de la chaleur, par échange thermique aux frontières du système. Elle est généralement notée Q ;
du travail, par action des forces de pression sur ces frontières, le travail des forces de pesanteur pouvant être négligé. Ce travail est généralement noté W en système fermé[1], et
en système ouvert[1], où on le qualifie de travail utile.
Pour calculer ces deux formes d'énergie mises en jeu dans une évolution, il ne suffit pas de connaître les états initial et final du système, mais il faut de plus connaître le chemin parcouru pendant la transformation.
Il s'agit d'un problème classique : comment peut-on calculer le changement global d'une variable au cours d'une évolution ?
La solution, si elle existe, relève du calcul différentiel. Elle consiste à décomposer l'évolution en ce qu'on appelle des évolutions élémentaires, pour lesquelles on peut écrire les équations de la physique en considérant que les grandeurs restent constantes. La prise en compte de la variation des propriétés se fait ensuite en « intégrant » les équations différentielles ainsi écrites, ce qui permet d'exprimer les lois suivies par l'évolution complète. Dans le cadre de cette présentation allégée, nous nous limitons à indiquer comment il faut procéder, mais il est inutile d'aller plus loin. |  Calculs différentiels |
Pour les systèmes thermodynamiques simples, on peut ainsi assez facilement montrer que, pour une évolution élémentaire en système ouvert,
et Q sont donnés par les expressions suivantes :
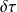= v dP ou dP =
Le travail utile reçu par les parois mobiles du système est égal au produit du volume massique du fluide par la variation élémentaire de la pression en son sein. Appliquée à un étage de compresseur, cette expression indique que le taux de compression réalisé est égal au produit de la densité
du fluide par le travail communiqué à l'arbre de la machine.
La seconde équation est :
= Cp dT – v dP
Cette dernière relation exprime simplement un fait expérimental essentiel, base de la thermodynamique des fluides compressibles : la chaleur
échangée avec l'extérieur se traduit par une modification linéaire de l'état thermodynamique du système, ici caractérisé par deux variables d'état, la température T et la pression P.
Si la pression reste à peu près constante, ce qui est le cas dans la plupart des échangeurs comme nous l'avons vu, dP = 0 et la variation de température du fluide est proportionnelle à la chaleur fournie au système.
Dans le cadre de cette présentation, nous ne chercherons pas à résoudre ces équations : nous déterminerons les énergies mises en jeu en utilisant des fonctions d'état bien choisies.
Insistons sur un point important : il ne faut pas confondre la chaleur Q et la température T, même si des relations existent entre les deux notions :
la température est une mesure du degré d'agitation des molécules du fluide de travail : plus elles sont agitées, plus sa température est élevée ;
la chaleur est un transfert d'énergie thermique d'un système à un autre lorsqu'il y a une différence de température entre eux.
Lors du changement d'état d'un fluide pur, sa température reste constante, alors qu'il échange de la chaleur avec l'extérieur.
