Cooling towers
Cooling towers
A cooling tower is a heat exchanger of a particular type that discharges heat in the surrounding air in the form of both sensible heat and latent heat due to the increase of its moisture.
By working this way, it is possible to cool a fluid at a temperature a few degrees above the ambient air wet bulb temperature (and possibly below its dry bulb temperature), at the cost of a water consumption of about 5% of that which water cooling would require. Both economically and environmentally, cooling towers are very interesting systems, in particular in hot and dry climates.
There are two main types of cooling towers, called direct contact or open-cycle, and indirect contact or closed-cycle.
Direct contact cooling towers

In a direct contact tower (Figure above), hot water is cooled in contact with ambient air either by spraying fine droplets, or by runoff along flow surfaces. Both fluids being in contact, heat is exchanged by convection, and part of the water vaporizes, thereby increasing the humidity. If it is not saturated, it starts to cool in an almost adiabatic process, before warming up along the saturation curve. Therefore water may come out at a temperature lower than ambient air.
Indirect contact cooling towers
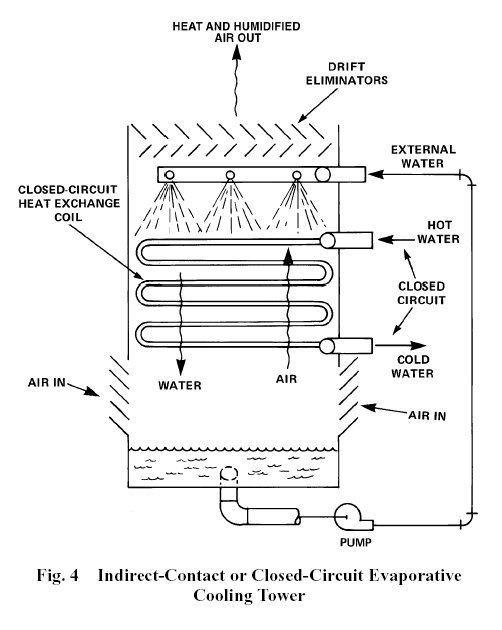
An indirect contact tower involves two circuits known as external and internal. In the latter, the cooling fluid, which can be arbitrary, remains confined in a tube bundle around which the external cooling circuit water runs. It warms on contact, then is cooled by exchange with ambient air by the same mechanism as in a direct contact tower.
Due to the evaporation of a portion of the water, the concentration of dissolved salts and the impurities, including biological, is expected to rise. We must firstly carry out blowdown, and also take care to avoid any risk of spread of Legionella.
Phenomenological model
A presentation of such a model iis presented in the guidance page for practical works on cooling towers.
Usual assumptions, due to Merkel, are:
air leaving the tower is nearly saturated
the interstitial film is saturated with moisture air, at the water temperature
the Lewis number is equal to 1;
thermal resistance on the liquid side is negligible compared to that on the air side (for indirect contact towers, it is assumed that the air-liquid film temperature gradient is equal to that of air-water cooling).
They lead to a model in which the main characteristic of the tower is a number of transfer units NTUm, the result of the integration of the equation:
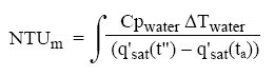
It is indeed an indicator of how difficult it is to realize the heat transfer in the cooling tower. Incorporating complex coupled phenomena of energy and mass exchange and dependent on technology implementation, it is not possible to give a simple expression.
We call the "approach" the pinch of the tower, i.e. the difference between the outlet temperature of the water and the wet bulb temperature of ambient air and the "range" the value of water temperature variation.
NTUm is usually given as a function of four variables:
the ratio of the mass flow rates of water and air;
the wet bulb air inlet temperature;
either the two water temperatures Twi (inlet) and Two (outlet);
the values of range (Twi - Two) and approach (Two - T'ai).
Behavior models
Many authors have investigated the modeling of cooling towers, and sought expressions of NTUm that are both easy to calculate and in agreement with experimental results. Since this is primarily an indicator of performance, it is not in itself unacceptable that there is a degree of arbitrariness in its definition, to the extent however that conventions are well specified.
Merkel model
Experience shows that when we modify the four input variables of a given cooling tower, NTUm takes different values, which follow a behavior similar to the following, n and m being with negative values between - 1.1 and -0.35, and C being between about 1 and 2.5. C, m and n are called the tower coefficients.

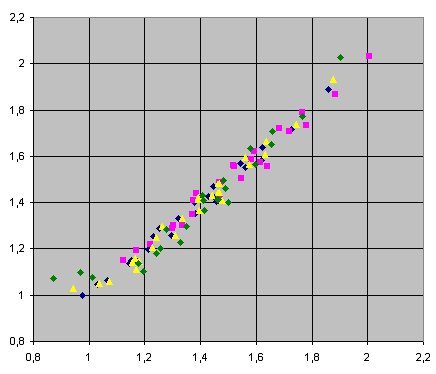
Mapping of manufacturer data and NTUm correlation
The figure above shows very good correspondence between the values of NTUm calculated for the same model of cooling tower ( Marley F1221) with four different fan engines (40, 50, 60 and 70 hp).
Cooling Technology Institute calculator
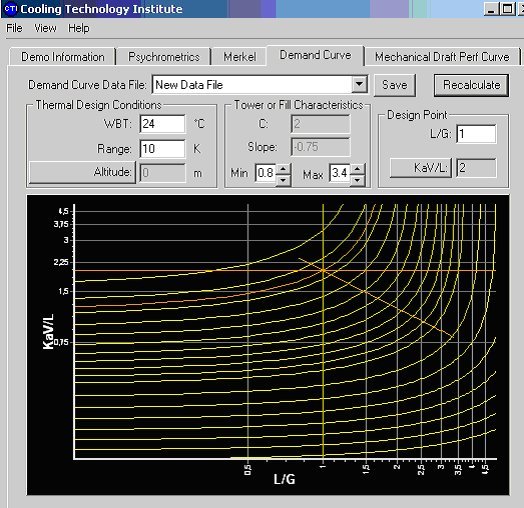
The Cooling Technology Institute has developed a tool called Toolkit, whose demo version is freely downloadable, which integrates the differential equation giving NTUm. A comparison with our results yields a very small difference, less than 2%, presumably due to a difference in fluid property modeling.
The mass flow of water being noted L and that of air G, the expression of NTUm in American literature is generally:
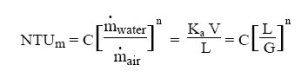
The cooling tower characteristics obtained have the appearance given above, in bi-logarithmic coordinates. Abscissa is the ratio of the mass flow of water to that of air L/G , and ordinate is NTUm. The design value is displayed in orange, as well as a curve representing the behavior model law.
This chart can be used to characterize a given tower:
the value of NTUm for design conditions is calculated;
the line of slope n and constant C is plotted and adjusted on the design point;
for other operating conditions, determined by the fluid flows, the abacus allows us to find, at abscissa L/G and on the tower characteristic line, the new values of NTUm and approach, which determines the outlet water temperature and therefore the capacity. The air outlet temperature is deduced. For another cooling or other air wet bulb temperature, it is possible to recalculate another abacus. Knowing the values of variables (NTUm, L/G) from the original chart, we get the new approach.
Analogies with heat exchangers
Since it is the change in enthalpy of saturated moist air which best characterizes the air thermodynamic behavior, a number of authors consider that it is as if water did exchange with a fictitious fluid whose specific heat at constant pressure is equal to the average heat capacity of moist saturated air Cp_asat, but it is also possible to express it in terms of specific heat of dry air.
We must therefore beware of the conventions used to avoid mistakes in calculations. The key is to be perfectly uniform throughout the approach: we must ensure that conventions used for identifying the values of C and n from experimental values are the same as those used to calculate epsilon and NTU.
The interested reader should refer to the referenced documents for more details.
It seems necessary to warn the reader: we tried to implement this approach on some experimental data either provided by the manufacturers or that we were able to get, and we realized that, when applied to NTUm, the correlations of the type Merkel lead to accurate reconstructions with values n and m close to those we have indicated. However they may be different when we use an (epsilon, NTU) approach similar to those of dry heat exchangers. We recommend extreme caution when using this analogy, and think it is better to apply the Merkel model which has been proven and is used by the profession. The calculations are slightly more complex, and can be made with small programs or Excel macros
Digital resources available in the portal
In this portal, the main resources for the cooling towers are:
a direct contact tower model;
an indirect contact tower model;
a guidance page for studying the coupling of a cooling tower to a refrigeration machine
References
D.R. BAKER, H.A. SHRYOCK. 1961. A comprehensive approach to the analysis of cooling tower performance. ASME Transactions, Journal of Heat Transfer (August), 339.
J.E. BRAUN, S.A. KLEIN, J.W. MITCHELL, "Effectiveness Models for Cooling Towers and Cooling Coils", ASHRAE Transactions, Vol. 92, Part 2, p. 164-174, 1989 ASHRAE Handbook 2000, "Cooling Towers", chapter 36
ASHRAE Handbook 2000, "Cooling Towers", chapter 36
F. KREITH, "The CRC Handbook of Thermal Engineering", CRC Press Springer, 3 "Cooling Towers", by A.F. Mills, Chapter 4.9, 1999
