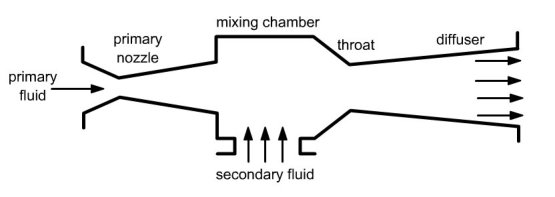
An ejector or injector (Figure below) receives as input two fluids normally gaseous but which may also be liquid or two-phase:

• the high pressure fluid called primary fluid or motive;

• the low pressure fluid, called secondary fluid or aspirated.

The primary fluid is accelerated in a converging-diverging nozzle, creating a pressure drop in the mixing chamber, which has the effect of drawing the secondary fluid. The two fluids are then mixed and a shock wave may take place in the following zone (throat in Figure below). This results in an increase in pressure of the mixture and reduction of its velocity which becomes subsonic. The diffuser then converts the residual velocity into increased pressure.

The ejector thus achieves a compression of the secondary fluid at the expense of a decrease in enthalpy of the primary fluid. This is the reason why an ejector is often called a thermocompressor.

The three most important parameters to characterize the overall efficiency of an ejector are:

• the entrainment ratio w, ratio of the secondary to primary mass flow-rates;

• the pressure lift ratio, the ratio of the static pressure at the outlet of the diffuser to the static pressure of the secondary fluid;

• a section ratio (minimal on maximum or primary flow on entrained flow etc.), which determines its geometry.

Ejector modeling is mostly based on the assumption that primary and secondary fluids can be treated as ideal gases in the mixing chamber, which is roughly justified given the low pressure therein. However, there are also cases where one of these fluids is liquid or two-phase, so that the mixture can be biphasic, and several hypotheses can be selected: either carry out calculations with the properties of a real fluid while using the hypothesis of a single-phase flow, or neglect the liquid phase when computing velocities, or consider an equivalent fluid.

The calculation of the ejector (one-dimensional model) is based on the following assumptions:

• the expansion of the primary and secondary fluids in the inlet nozzle is assumed to be adiabatic, taking into account the irreversibilities by an isentropic efficiency;

• the pressure remains constant in the mixing chamber ;

• when the mixed flow is supersonic, a normal shock can take place in the mixing chamber, which slows down the fluid and creates an overpressure;

• compression in the diffuser is assumed to be adiabatic, taking into account the irreversibilities by an isentropic efficiency;

• fluid properties are uniform in any section.

The model we used is that proposed by Li and Groll (2005), which presents the advantage of being formulated in a manner independent of fluid properties. We have slightly reformulated and expanded it to take account of any shock, these authors implicitly limiting themselves to cases where the mixed flow is subsonic.

Two versions of this model are available in the Thermoptim model library , one for ideal gases, the other for real condensable fluids.

The ejectors are static devices that allow one to compress a fluid without using mechanical compression. They can therefore replace compressors in many applications such as mechanical vapor compression , refrigeration and heat pump cycles, the extraction of noncondensable gases from the condenser of a steam cycle