Echangeurs de chaleur monophasiques
Présentation
Dans ce fil d'Ariane pédagogique sur les échangeurs de chaleur, après avoir succinctement rappelé ce que sont de tels composants et donné quelques éléments de théorie sur la manière dont ils peuvent être calculés, nous détaillons le calcul et le dimensionnement d'un échangeur servant à refroidir de l'air sortant d'un compresseur.
Il s'agit d'un exemple destiné à bien faire comprendre quels sont les problèmes posés et comment ils peuvent être résolus, sans que le système d'ensemble soit trop compliqué. Pour des spécialistes, il paraîtra sans doute un peu simpliste, mais pour des débutants, il se révèle déjà relativement difficile à traiter complètement.
Il fait appel à la version 1.7 de Thermoptim actuellement en cours de développement.
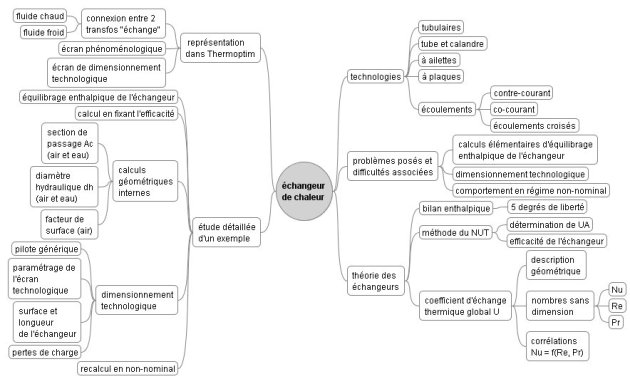
La carte ci-dessous résume l'essentiel des notions qui seront abordées ici.
Qu'est-ce qu'un échangeur de chaleur ?
Sur le plan fonctionnel, les échangeurs de chaleur sont des appareils qui servent à transférer de la chaleur entre deux fluides à des températures différentes.
Un exemple assez bien connu d'échangeur de chaleur est le "radiateur" d'une automobile, qui permet de refroidir le moteur en rejetant dans l'atmosphère la chaleur excédentaire. Il évite ainsi une détérioration du moteur par surchauffe des pièces mécaniques. En cas de dysfonctionnement de ce composant, un accident grave comme le blocage du moteur par "coulage" de bielle peut survenir.
Sur le plan technologique, bien qu'il existe une très importante variété de modèles d'échangeurs, les quatre principales catégories utilisées dans les systèmes énergétiques sont les suivantes :
les échangeurs tubulaires
les échangeurs à tube et calandre
les échangeurs à ailettes
les échangeurs à plaques
Généralement, les deux fluides ne sont pas en contact, et le transfert s'effectue à travers une surface d'échange. Au sein de la paroi séparatrice, le mécanisme de transmission de la chaleur est la conduction, et, sur chacune des deux surfaces de contact avec les fluides, ce sont presque toujours les phénomènes de convection qui prédominent.
Dans de nombreux cas, les fluides restent monophasiques, qu'ils soient gazeux ou liquides. Il existe toutefois trois grandes catégories d'échangeurs dans lesquelles surviennent des changements de phase : les vaporiseurs ou évaporateurs où l'on vaporise un liquide, les condenseurs où une vapeur est liquéfiée, et les vapocondenseurs dans lesquels les deux fluides changent de phase. Nous nous limiterons ici aux échangeurs monophasiques.
Le schéma ci-dessous permet de préciser les notations que nous utiliserons. On repère le fluide chaud par l'indice c, et le fluide froid par l'indice f. Les principales variables qui doivent être prises en compte sont :
les débits masses mc et mf qui les traversent ;
les températures d'entrée Tce et Tfe et de sortie Tcs et Tfs des deux fluides.

Importance pour les systèmes énergétiques
En pratique, les échangeurs de chaleur revêtent une grande importance dans de nombreux systèmes énergétiques qui sont le siège de transferts de chaleur, notamment lorsque l'on cherche à récupérer de l'énergie thermique.
Par ailleurs, les échangeurs peuvent jouer un rôle critique dans les performances des systèmes énergétiques mettant en jeu des échanges internes, comme les cycles à régénération ou combinés, dont l'optimisation demande de réduire au minimum les irréversibilités internes liées aux différences de température dans les échangeurs.
Typologie des problèmes posés et difficultés associées
L'étude des échangeurs dans un système énergétique présente des niveaux de difficulté très différents selon les objectifs que l'on poursuit.
L'approche la plus élémentaire, très simple à mettre en pratique, consiste à équilibrer l'échangeur sur le plan enthalpique en déterminant par exemple la température de sortie de l'un des fluides lorsque les températures d'entrée et les débits des deux fluides sont connus, ainsi qu'une des températures de sortie.
Le problème peut être posé de manière inverse, si les deux températures de sortie sont connues et une seule d'entrée. L'approche est alors aussi simple.
On peut en effet montrer qu'un échangeur possède cinq degrés de liberté et qu'une fois cinq grandeurs imposées parmi les températures d'entrée et de sortie et les débits, la sixième s'en déduit directement.
Il est aussi coutumier de caractériser un échangeur par une efficacité ou bien un écart de température minimum entre les deux fluides (appelé pincement[1]). La résolution de ce problème est elle aussi assez simple si quatre autres grandeurs sont connues.
Nous qualifierons ce type d'étude de calculs élémentaires d'équilibrage enthalpique de l'échangeur.
Précisons que, très souvent dans l'étude des systèmes énergétiques, les calculs sur les échangeurs ne sont pas poussés plus avant. Ils fournissent déjà en effet suffisamment d'informations pour mener des premières analyses de nombreux cycles, notamment au niveau fonctionnel, en dehors de considérations technologiques précises.
La théorie montre comme nous le verrons que cette approche permet de caractériser un échangeur par ce que l'on appelle le produit UA de son coefficient d'échange thermique interne entre les deux fluides U par sa surface d'échange A.
Pour aller plus loin et déterminer la surface d'échange requise, il faut effectuer des calculs beaucoup plus compliqués, qui requièrent une connaissance approfondie du fonctionnement des échangeurs, ceci afin d'estimer aussi précisément que possible la valeur de U.
Il y a réellement un saut qualitatif très important entre le calcul élémentaire d'équilibrage de l'échangeur et ce que nous appellerons son dimensionnement technologique.
Il s'agit d'ailleurs d'un problème général dans les études de systèmes énergétiques : tant que l'on se contente d'effectuer des études de cycles sans chercher à dimensionner les composants sur le plan géométrique, les calculs restent beaucoup plus simples que lorsque l'on désire analyser finement leur comportement interne.
Une fois la surface d'un échangeur de chaleur déterminée, ce qui permet de le caractériser sur le plan géométrique de manière détaillée, un autre problème reste à traiter : celui de son comportement lorsque ses conditions de fonctionnement diffèrent de celles qui ont servi à le dimensionner. Comment l'échangeur s'adapte-t-il à des modifications des débits et températures d'entrée des fluides qui le traversent ?
Nous qualifions cette problématique d'étude de son comportement en régime non-nominal.
Elle peut être d'un niveau de complexité supérieur à celle du dimensionnement technologique, du fait qu'elle peut demander la résolution de systèmes d'équations non linéaires de rang élevé lorsque plusieurs composants sont couplés entre eux.
Eléments de théorie des échangeurs : calcul de UA, de epsilon et de NUT
Compte tenu de l'objectif de ce fil d'Ariane pédagogique, qui est de constituer un guide pour aider les enseignants et les élèves à comprendre comment les notions s'enchaînent, nous nous contenterons de poser les principaux jalons concernant la théorie des échangeurs, renvoyant le lecteur d'une part à la fiche thématique sur le sujet, et d'autre part à des ouvrages spécialisés.
Trois hypothèses de base sont généralement retenues pour modéliser un échangeur :
en première approximation, il peut être considéré comme isobare (plus précisément les pertes de charge restent faibles) ;
il est globalement adiabatique, c'est-à-dire qu'il n'y a aucun échange de chaleur avec l'environnement ;
les coefficients d'échange thermique et les propriétés thermophysiques des fluides gardent une valeur constante dans la totalité de l'échangeur (cette hypothèse n'est pas reprise dans Thermoptim, où ces propriétés dépendent de la température et donc évoluent entre l'entrée et la sortie de l'échangeur).
D'une manière générale, le dimensionnement des échangeurs est un compromis entre des objectifs contradictoires, dont les principaux sont les suivants :
une grande surface d'échange est souhaitable pour augmenter l'efficacité des échangeurs, mais elle se traduit par des coûts élevés ;
de faibles sections de passage des fluides permettent d'augmenter les valeurs des coefficients d'échange thermique, et donc de réduire les surfaces, mais elles font aussi croître les pertes de charge.
Le flux de chaleur échangé
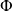 peut s'exprimer principalement de trois manières équivalentes, selon qu'on l'exprime au niveau du fluide chaud, du fluide froid ou entre les deux fluides :
peut s'exprimer principalement de trois manières équivalentes, selon qu'on l'exprime au niveau du fluide chaud, du fluide froid ou entre les deux fluides :
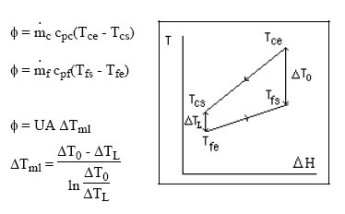
Les deux premières équations traduisent la chaleur perdue par le fluide chaud et reçue par le fluide froid, tandis que la troisième exprime ce flux comme étant proportionnel au coefficient d'échange thermique U, à la surface de l'échangeur A et à l'écart moyen de température entre les deux fluides, appelé différence de température moyenne logarithmique
 .
.
En effet, étant donné que les températures varient le long de l'échangeur, une simple moyenne ne suffit pas à déterminer l'écart moyen de température entre les deux fluides : la valeur à prendre en compte est donnée par la dernière équation ci-dessus, où
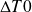 et
et
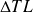 sont les différences de température des fluides respectivement à l'entrée et à la sortie de l'échangeur, avec la convention :
sont les différences de température des fluides respectivement à l'entrée et à la sortie de l'échangeur, avec la convention :
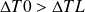 .
.
Classiquement, le dimensionnement des échangeurs s'est longtemps fait en utilisant la méthode de la différence de température moyenne logarithmique
 , mais celle-ci n'est pas toujours très facile à mettre en oeuvre.
, mais celle-ci n'est pas toujours très facile à mettre en oeuvre.
La méthode de calcul que nous préconisons est celle du NUT, ou encore Nombre d'Unités de Transfert, mise au point plus récemment et plus facile à utiliser en pratique. Nous nous contenterons ici d'une présentation très synthétique, renvoyant le lecteur intéressé par plus de développements à l'édition 2009 du livre Systèmes Energétiques.
Par définition, NUT est défini comme le rapport entre le produit UA de l'échangeur et le débit de capacité thermique le plus faible :
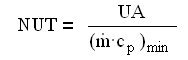
On appelle R le rapport (inférieur à 1) du débit de capacité thermique le plus faible au plus fort :
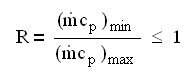
Soit
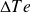 la différence entre les températures d'entrée des deux fluides, et
la différence entre les températures d'entrée des deux fluides, et
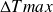 l'écart de température maximal au sein de chacun des deux fluides et non entre eux.
l'écart de température maximal au sein de chacun des deux fluides et non entre eux.
On appelle
 l'efficacité de l'échangeur, définie comme étant le rapport de
l'efficacité de l'échangeur, définie comme étant le rapport de
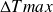 à
à
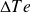 :
:

Avec ces définitions, il est possible de montrer qu'il existe une relation générale du type :
 = f(NUT, R, configuration d'écoulement)
= f(NUT, R, configuration d'écoulement)
Dans un échangeur, l'écoulement des deux fluides peut s'effectuer dans de multiples dispositions relatives : parallèlement, à contre-courant, de manière croisée...
On peut facilement démontrer que, sur le plan thermodynamique, l'échangeur le plus performant est l'échangeur à contre-courant, mais d'autres préoccupations que l'efficacité thermodynamique entrent en ligne de compte lorsque l'on conçoit un échangeur : les températures maximales admissibles dans l'un des fluides, ou plus souvent des considérations d'encombrement, de poids ou de prix de revient. Dans cette présentation simplifiée, les calculs seront effectués pour la configuration à contre-courant, même si l'exemple traité correspond à des courants croisés. L'erreur commise reste faible.
En pratique, pour appliquer la méthode du NUT, il suffit de disposer d'une série de relations correspondant aux configurations d'écoulement représentatives des échangeurs étudiés, et le dimensionnement d'un échangeur se fait sur la base, d'une part des équations de bilan, et d'autre part de ces relations.
En mode dimensionnement, connaissant les débits des deux fluides, leurs températures d'entrée et le flux à échanger, on opère de la manière suivante :
on commence par déterminer les températures de sortie des fluides à partir de l'équation de bilan ;
on en déduit les débits de capacité thermique m cp des fluides et leur rapport R ;
on calcule l'efficacité
 à partir de
à partir de
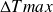 et
et
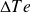 ;
;
on détermine la valeur du NUT à partir de la relation (NUT,
 ) appropriée ;
) appropriée ;
on calcule le produit UA à partir de l'équation définissant NUT.
En régime non-nominal, si l'on connaît le produit UA, l'équation définissant NUT donne sa valeur, et on détermine celle de
 à partir de la relation (NUT,
à partir de la relation (NUT,
 ) appropriée.
) appropriée.
L'équation de bilan permet alors de calculer le flux transféré.
Éléments de thermique : calcul du coefficient d'échange thermique global U
La méthode du NUT ne fournit que le produit UA du coefficient global d'échange par la surface de l'échangeur, sans que les deux termes soient évalués séparément.
Pour pouvoir dimensionner l'échangeur, c'est-à-dire calculer sa surface, il faut d'une part choisir sa configuration géométrique, et d'autre part calculer le coefficient global d'échange U, qui est fonction de cette configuration et des propriétés thermophysiques des fluides.
Le coefficient d'échange thermique global U dépend de la répartition des résistances thermiques dans l'échangeur. Si les surfaces d'échange sont égales pour les deux fluides, sa valeur est donnée par l'équation ci-dessous, où e/l représente la résistance de paroi d'épaisseur e, lambda étant ici la conductivité du matériau la composant :
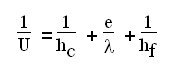
Les valeurs des coefficients de convection hc et hf sont quant à elles fonctions des propriétés thermophysiques des fluides et des configurations d'échange, les régimes convectifs dépendant fortement de la vitesse d'écoulement.
Leur détermination relève de la mécanique des fluides et de la thermique de la convection, notamment turbulente.
Leur mise en équations conduit à des représentations très complexes qui n'ont généralement pas de solutions analytiques. Compte tenu de cette difficulté, on a coutume d'avoir recours aux lois de la similitude qui permettent d'obtenir des résultats raisonnablement précis.
Sans entrer dans les détails qui débordent du cadre de cette présentation, les lois de la similitude établissent que l'échange thermique entre un fluide et une paroi peut être caractérisé par plusieurs nombres adimensionnels appelés :
nombre de Nusselt Nu ;
nombre de Reynolds Re ;
et nombre de Prandtl Pr.
L'expression donnant le nombre de Nusselt est la suivante, lambda étant la conductivité du fluide et dh le diamètre hydraulique :

Re est généralement défini en fonction de de la masse volumique
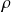 , de la vitesse d'écoulement C, du diamètre hydraulique dh et de la viscosité cinématique
, de la vitesse d'écoulement C, du diamètre hydraulique dh et de la viscosité cinématique
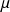 .
.
En faisant apparaître la section de passage dévolue au fluide Ac, il peut aussi s'exprimer en fonction du débit-masse, du diamètre hydraulique dh et de la viscosité cinématique
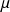 .
.

Pr dépend de la viscosité cinématique
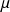 , de la capacité thermique massique cp et de la conductivité du fluide
, de la capacité thermique massique cp et de la conductivité du fluide
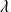 , c'est-à-dire de ses seules propriétés thermophysiques.
, c'est-à-dire de ses seules propriétés thermophysiques.

Les lois de la similitude permettent d'établir que le nombre de Nusselt est une fonction des nombres de Reynolds et de Prandtl.
C1, a, b, et c étant des constantes, le nombre de Nusselt est en effet presque toujours donné par une relation du type :
La correction de viscosité se fait par rapport à la température de la paroi. Les coefficients C1, a et b varient selon les configurations rencontrées, et le terme supplémentaire pour tenir compte des variations de la viscosité est souvent négligé.
D'une manière générale, l'exposant du nombre de Reynolds est compris entre 0,5 et 0,8, et celui du nombre de Prandtl entre 0,33 et 0,4.
De telles corrélations, dont l'existence est validée par la théorie, sont en pratique mises en évidence expérimentalement, en réalisant un très grand nombre d'essais avec de nombreux fluides, pour des diamètres hydrauliques variables, des vitesses et des flux échangés différents...
Des régressions sont ensuite effectuées numériquement pour identifier les paramètres de formules du type ci-dessus.
Le régime d'écoulement a une influence importante sur la valeur de Re et donc de Nu.
Dans le cas où Re est inférieur à 2000, le régime est laminaire, et si Re est supérieur à 5000, il est turbulent, avec une zone de transition, ces frontières n'étant pas parfaitement stables. La turbulence favorise les échanges thermiques, mais sa contrepartie est une élévation des pertes de charge.
Une page spécifique de ce portail est consacrée à la présentation des corrélations qui ont été implémentées dans les classes externes de Thermoptim pour permettre l'étude du dimensionnement des échangeurs de chaleur et de leur comportement en régime non-nominal.
Éléments de mécanique des fluides : calcul des pertes de charge
On appelle perte de charge la diminution de pression qui prend place lors de l'écoulement d'un fluide dans une canalisation du fait des frottements visqueux et des chocs.
Même si elles sont souvent considérées comme faibles, les pertes de charge ne sont pour autant pas toujours négligeables.
On distingue généralement deux types de pertes de charge :
les pertes de charge régulières ou linéiques, proportionnelles à la longeur de la canalisation
les pertes de charge singulières proviennent des singularités rencontrées, comme des raccords, coudes, tés ou vannes.
Pertes de charge régulières
C est la vitesse du fluide, v son volume massique, et L la longueur de la canalisation, elles s'expriment généralement sous la forme :
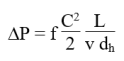
f est le coefficient de frottement, donné par des corrélations et de la rugosité relative RR. Pour une première évaluation rapide, il pourra être pris égal à 0,02 environ pour un tube lisse.
En régime laminaire, pour un fluide monophasique, les pertes de charge sont proportionnelles au débit et à la viscosité du fluide : f = 64/Re.
En régime turbulent (Re>2100), toujours pour un fluide monophasique, le coefficient de frottement est donné par l'équation de Colebrook :
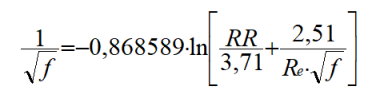
Dans cette équation, RR=
 /dh est la rugosité relative,
/dh est la rugosité relative,
 étant la rugosité absolue du tube.
étant la rugosité absolue du tube.
Pour d'autres types d'écoulement, diverses corrélations peuvent être trouvées dans la littérature. Celles qui sont implémentées dans les classes externes de Thermoptim sont indiquées dans cette page du portail.
Pertes de charge singulières
Les pertes de charge singulières proviennent des singularités rencontrées, comme des raccords, coudes, tés ou vannes. Elles s'expriment sous la forme :
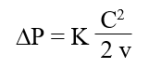
K est un coefficient qui dépend du type de singularité.
La vitesse C à prendre en compte est selon les cas relative aux conditions amont ou aval.
Pour les cônes ou convergents ou divergents, la perte de charge est proportionnelle à la différence des carrés des vitesses en amont et en aval.
Le coefficient K représente la fraction de l'énergie cinétique du fluide qui est transformée en perte de charge. Les pertes de charge singulières ne deviennent importantes que pour des écoulements très fortement turbulents.
Représentation dans Thermoptim
Rappelons qu'une transfo "échange" sert à calculer l'échauffement ou le refroidissement d'un fluide entre deux états définis par les points amont et aval.
Elle est symbolisée dans Thermoptim par l'icône :
Dans Thermoptim, un échangeur n'est pas représenté par un composant particulier, mais par une connexion établie entre deux transformations "échange" qui représentent l'une le fluide chaud, et l'autre le fluide froid.
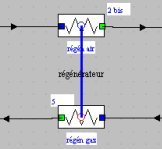
Pour modéliser les échangeurs dans l'éditeur de schémas, on utilise donc des liens non orientés reliant entre eux deux composants de type "échange".
Compte tenu des hypothèses retenues, l'échangeur est nécessairement équilibré sur le plan enthalpique, c'est-à-dire que l'enthalpie cédée par le fluide chaud est exactement égale à celle reçue par le fluide froid.
Etant donné qu'il y a quatre températures (deux pour chaque fluide) et deux débits, calculer un échangeur comporte comme nous l'avons dit cinq degrés de liberté une fois la conservation de l'enthalpie assurée. On peut par ailleurs montrer que l'un des deux débits au moins doit être spécifié, faute de quoi le problème est indéterminé.
Thermoptim propose donc de multiples options de dimensionnement correspondant à ces degrés de liberté.
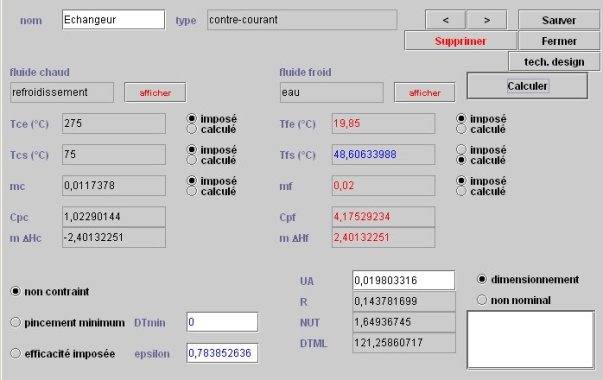
La figure ci-dessus montre l'écran d'un échangeur dans Thermoptim. Il comporte les informations relatives au fluide chaud dans sa partie centrale gauche, tandis que celles relatives au fluide froid sont à droite.
Outre les valeurs des températures, débits, chaleurs massiques et enthalpies mis en jeu, apparaissent des options portant sur les températures et les débits qui servent à gérer le calcul des échangeurs, en permettant de distinguer, parmi les variables du problème, celles qui sont imposées et celles qui doivent être calculées.
Dans la partie inférieure gauche, apparaissent trois boutons qui peuvent permettre de spécifier l'absence ou la présence de contraintes implicites sur les températures.
Dans la partie inférieure droite sont placées les options permettant de définir le mode de calcul ("dimensionnement" ou "non nominal").
Les résultats du dimensionnement de l'échangeur sont affichés dans les champs en bas au centre de l'écran, fournissant les valeurs de UA, de R, de NUT et de DTML. Le champ de UA est éditable, ce qui permet comme nous le verrons plus loin de le modifier pour effectuer des calculs en régime non-nominal.
Etude progressive et détaillée d'un exemple d'échangeur
Equilibrage enthalpique de l'échangeur
Considérons un échangeur à tubes et ailettes destiné à refroidir à 75 °C un débit d'air de 0,66 kg/mn (11,738 g/s) sortant d'un compresseur à 5 bars et 275 °C grâce à un débit de 1,17 kg/mn (20 g/s) d'eau froide.
Le flux thermique à évacuer est égal à 2,4 kW environ : 0,011738 . 1,022 (275 - 75), ce qui conduit à un échauffement de l'eau voisin de 28,75 °C : 2,4/0,02/4,1753.
L'échangeur peut être facilement modélisé dans Thermoptim, conduisant à l'écran de la figure ci-dessus, et au synoptique de la figure ci-dessous.
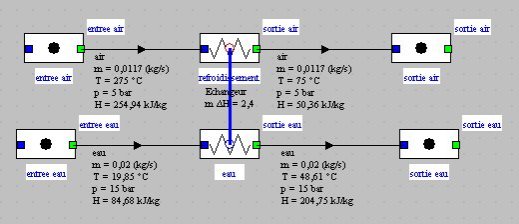
Calcul en fixant l'efficacité
Pour dimensionner l'échangeur, il est fréquent de se fixer une efficacité, par exemple égale à 0,84 au lieu de la valeur de 0,78 déterminée précédemment. Le synoptique et l'écran de l'échangeur sont alors donnés ci-dessous : la puissance thermique est nettement augmentée.
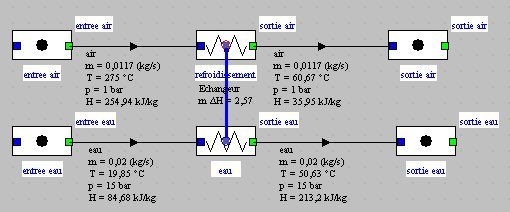
Synoptique pour une efficacité d'échangeur égale à 0,84.

Les principales grandeurs de dimensionnement sont ainsi calculées et affichées dans la partie inférieure de l'écran :
le produit UA vaut 0,02386 ;
R, rapport des débits calorifiques, vaut 0,1436 ;
NUT, le nombre d'unités de transfert, est égal à 2 environ ;
DTML, écart de température moyen logarithmique, vaut 107,7 °C.
Jusqu'à présent, nous n'avons utilisé que les fonctionnalités classiques (écrans phénoménologiques) du progiciel, et nous ne parvenons à obtenir que le produit UA du coefficient d'échange thermique par la surface de l'échangeur, sans qu'il soit possible de déterminer séparément les valeurs de chacun de ces deux facteurs. Ici UA = 0,02386 kW/K, ou 23,86 W/K).
Nous allons maintenant montrer comment il est possible d'affiner nos analyses.
Calculs géométriques internes
Supposons que notre échangeur est constitué de tubes et ailettes, l'eau froide passant dans un serpentin composé de plusieurs passes de deux tubes en parallèle comme le montre la figure ci-dessous où ils apparaissent horizontalement, en bleu. Le diamètre des tubes est de 15 mm, et leur épaisseur de 1,5 mm. Des ailettes, représentées verticalement et en gris, sont serties perpendiculairement autour des tubes. L'espacement e entre ces ailettes est de 3 mm, leur demi-hauteur h de 1 cm, leur profondeur l de 2 cm, et leur épaisseur a de 0,3 mm.
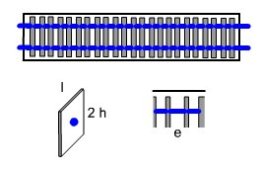
Pour le calcul des coefficients d'échange thermique et des pertes de charge, outre la surface de l'échangeur A, deux grandeurs sont toujours nécessaires : la section de passage dévolue au fluide Ac, et le diamètre hydraulique dh.
Lorsque, comme c'est le cas dans cet exemple, les coefficients d'échange thermique des fluides sont très différents, on a recours à des dispositifs divers comme des ailettes pour compenser l'écart entre leurs valeurs. On parle alors de surfaces étendues, qui peuvent être caractérisées par un facteur de surface f et un rendement d'ailette eta.
A l'intérieur des tubes, dh est donné, et le calcul de Ac est très simple : il est égal au produit du nombre de tubes par la section unitaire. Pour un diamètre extérieur des tubes de 15 mm et une épaisseur de 1,5 mm, le diamètre intérieur vaut 12 mm. Un calcul simple montre que, pour deux tubes, Ac vaut 0,000226195 m2.
A l'extérieur des tubes, les calculs sont un peu plus compliqués. Une des grandeurs à déterminer est le nombre d'ailettes Na, et l'autre le nombre de passes global. Elles ne peuvent être déterminées que par itération, notamment la première, qui influence directement la section de passage dévolue à l'air.
Pour éviter de trop longues explications, nous retiendrons tout de suite le résultat obtenu, à savoir 90 ailettes.
Détermination de la section de passage relative à l'air
La section de passage par tube est égale à :
Ac0 = (2 h - d) e = 0,000015 m2
Le nombre de tubes étant égal à 2, la section de passage globale vaut
Ac = 0,0027 m2
Détermination du diamètre hydraulique relatif à l'air
Le périmètre mouillé vaut quant à lui :
p = 2 (2 h +e) = 0,046 m
Ce qui permet de calculer le diamètre hydraulique externe :
dh = 4 Ac/p = 0,001304348 4 m
Détermination du facteur de surface relatif à l'air
Il faut commencer par calculer la surface initiale du tube, soit pi d e :
S = 0,000141372 m2
et la surface étendue qui vaut, par ailette :

Se = 0,000573805 m2
Le facteur de surface, rapport de ces deux valeurs, s'en déduit :
f = 4
Le rendement d'ailette ne sera pas calculé ici, mais simplement estimé égal à 0,8.
Par ailleurs, la longueur de l'échangeur vaut :
Le = Na (e + a) = 0,297 m
En utilisant les écrans de dimensionnement technologique de Thermoptim, nous allons maintenant pouvoir calculer le coefficient d'échange thermique global et en déduire la surface nécessaire pour transmettre la puissance souhaitée.
Lorsque l'on se contente de vouloir effectuer le dimensionnement technologique d'un projet qui ne met en oeuvre que des composants du noyau de Thermoptim, leurs écrans technologiques peuvent être créés automatiquement en utilisant le pilote générique, sans avoir besoin d'en programmer un particulier.
Pour charger le pilote générique, ouvrez l'écran de pilotage à partir du menu Spécial du simulateur, et sélectionnez "generic techno design pilot ".
Une fois l'écran du pilote générique ouvert, cliquez sur le bouton "Set the technological design screens".
Une ligne apparaît correspondant à l'échangeur, comme dans la figure ci-dessous. Sélectionnez-la.
Son type est par défaut HeatEx, et son TechnoDesign technoHx. Etant donné qu'il s'agit d'un échangeur simple, ils conviennent parfaitement. Un double-clic sur cette ligne permettrait de changer le type de TechnoDesign, mais ce n'est pas ici nécessaire.
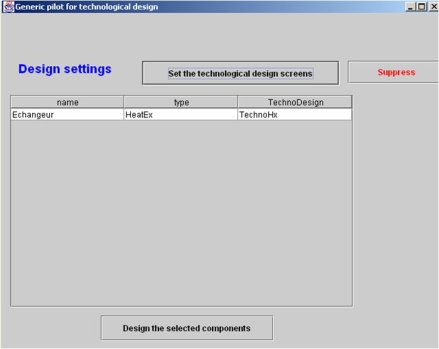
Pour faire apparaître l'écran technologique, le plus simple est ici d'ouvrir l'écran de l'échangeur et de cliquer sur le bouton "tech. design" situé juste au dessus du bouton "Calculer".
L'écran technologique par défaut est alors affiché comme ci-dessous. Nous allons maintenant voir comment le paramétrer.
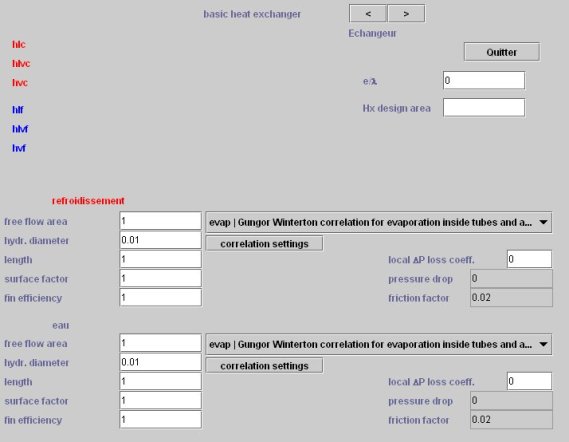
Ecran technologique par défaut de l'échangeur
L'écran de dimensionnement technologique de l'échangeur contient dans sa partie inférieure gauche les deux zones relatives à chaque transfo "échange".
On y retrouve, pour chacun des deux fluides, les quatre paramètres Ac, dh, f et eta. On leur ajoute la longueur de l'échangeur pour certains calculs, notamment des pertes de charge.
Dans l'écran de dimensionnement technologique des échangeurs ci-dessus, les conventions suivantes sont adoptées :
"free flow area" représente la section de passage Ac ;
"hydr. diameter" est le diamètre hydraulique habituel dh ;
"length" est la longueur de l'échangeur ;
"surface factor" est le facteur de surface f pour les surfaces étendues ;
"fin efficiency" est le rendement d'ailettes eta ;
la résistance de paroi e/lambda est saisie dans la partie supérieure droite de l'écran, sous le bouton "Quitter". Elle permet de prendre en compte des résistances d'encrassement si on le souhaite. Dans cet exemple nous les négligerons.
Les valeurs des paramètres de dimensionnement technologique doivent être saisies pour chacun des deux fluides, ainsi que leur configuration d'écoulement choisie dans la liste proposée, ici "ext_tube | Colburn correlation..." pour l'air de refroidissement, et "int_tube | Mac Adams correlation..." pour l'eau à l'intérieur des tubes.
Les valeurs qui ont été déterminées ci-dessus doivent être entrées dans l'écran de dimensionnement technologique de l'échangeur. Pour le moment, les longueurs des échangeurs ne sont pas connues, puisque le nombre de passes n'est pas déterminé. In fine, on verra qu'il est égal à 3. Les valeurs entrées dans l'écran ci-dessous correspondent à cela.
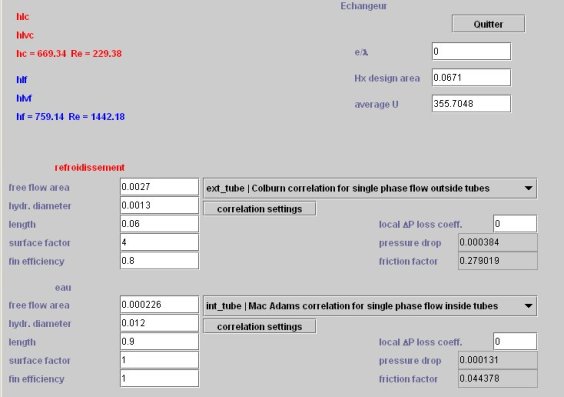
Ecran technologique de l'échangeur paramétré
Une fois les paramètres entrés, revenez sur l'écran du pilote générique, puis cliquez sur le bouton "Design the selected component".
Cela a pour effet de réaliser le dimensionnement technologique.
Les résultats sont affichés sur l'écran technologique : la surface d'échange nécessaire est ici égale à 0,067 m2, les coefficients d'échange valant 669 W/m2/K côté air, et 759 côté eau
Le nombre de passes se déduit de ces résultats. Il est égal au rapport de la surface de l'échangeur par la surface interne des deux tubes d'eau, voisin de 3 compte tenu des valeurs géométriques retenues.
Nous disions plus haut que ce nombre de passes et le nombre d'ailettes ne pouvaient être trouvés que par itération. En effet, le premier doit être un nombre entier, et le second fixe la section de passage dévolue à l'air. On peut donc avoir à tester plusieurs jeux de valeurs avant d'entrouver un qui soit cohérent.
Les longueurs à prendre en compte pour le calcul des pertes de charge peuvent être déterminées maintenant : 3 x Le = 90 cm pour les tubes (en négligeant les coudes entre les nappes), et 3 x l = 6 cm pour les ailettes.
L'échangeur sera donc constitué de deux tubes de 90 cm de longueur chacun disposés en serpentin sur 3 nappes et traversant au total 540 plaques de tôle carrées de 2 cm de côté séparées les unes des autres de 3 mm.
Les valeurs des pertes de charge apparaissent en bars dans la partie droite de l'écran technologique ("pressure drop"). Elles sont comme on peut le voir tout à fait négligeables dans notre cas.
Les fichiers correspondant à cet exemple sont disponibles pour téléchargement .
Calculs en régime non-nominal
En régime non-nominal, on connaît généralement les températures d'entrée et les débits des fluides qui traversent l'échangeur. Une première estimation de U peut donc être effectuée, même si elle peut être affinée quand les températures de sortie sont connues.
La surface d'échange étant connue, le produit UA peut être déterminé, ce qui donne la valeur du NUT.
On peut alors calculer celle de epsilon à partir de la relation (NUT, e) appropriée.
L'une des deux températures de sortie est obtenue à partir de la définition d'e, et le bilan enthalpique fournit l'autre.
Sur le plan pratique, il y a deux principales façons d'opérer :
soit en modifiant le UA et en recalculant l'échangeur en mode non-nominal ;
soit en recalculant directement le NUT et epsilon, notamment si les conditions d'entrée peuvent être modifiées. C'est le cas en particulier des échangeurs diphasiques, dont l'équilibre thermique fixe la température de changement d'état et donc la pression, ce qui a pour effet de modifier à la fois les conditions de sortie et d'entrée.
La première manière, la plus simple, consiste à utiliser l'option de calcul en non-nominal de l'écran des échangeurs. Cela peut être fait directement à la main, en entrant la nouvelle valeur de UA dans le champ correspondant, ou bien, par programmation.
Une fois l'échangeur dimensionné, son comportement en régime non-nominal peut ainsi être étudié directement à partir de son écran dans le simulateur.
Le mode de calcul "non nominal" permet en effet de calculer, par la méthode du NUT, l'échangeur en régime non nominal en considérant que ses deux températures d'entrée et ses deux débits sont imposés.
Thermoptim effectue une mise à jour des liens amont de l'échangeur à partir des transfos, puis effectue le calcul des températures aval et équilibre le bilan sur le plan enthalpique, le UA ayant la valeur entrée dans le champ de l'écran de l'échangeur. Les points et les transfos associés au module sont mis à jour en fonction des résultats. Aucune correction n'est cependant automatiquement apportée sur UA pour tenir compte de l'évolution des coefficients d'échange en fonction des débits et des températures.
Il faut donc effectuer un nouveau calcul de l'échangeur, estimer la valeur de U qui en résulte, et modifier UA en conséquence, puis relancer le calcul, en réitérant l'opération jusqu'à stabilisation des valeurs.
A titre d'exemple, examinons comment se comporterait notre échangeur si le débit et la température de l'air entrant étaient modifiés, passant respectivement de 0,01174 à 0,1 kg/s et de 275 à 300 °C.
Opérez comme suit :
modifiez les conditions d'entrée dans l'échangeur dans Thermoptim, choisissez l'option "non-nominal" au lieu de dimensionnement dans l'écran de l'échangeur ;
recalculez plusieurs fois l'échangeur , jusqu'à stabilisation des valeurs ;
cliquez enfin sur le bouton "Design the selected component" de l'écran du pilote générique.
La nouvelle valeur de U est calculée : elle vaut 338,7 kW/m2/K.
En multipliant cette valeur par la surface de l'échangeur, vous obtenez une nouvelle valeur de UA , égale à 0,022725, que vous entrez dans le champ correspondant de l'écran de l'échangeur.
Répétez les opérations 1 à 3 : une estimation plus précise de U est obtenue, tenant compte du nouveau paramétrage. Il vaut 338.66 kW/m2/K.
Remodifiez UA en conséquence, ce qui vous conduit aux écrans d'échangeur et de TechnoDesign ci-dessous.
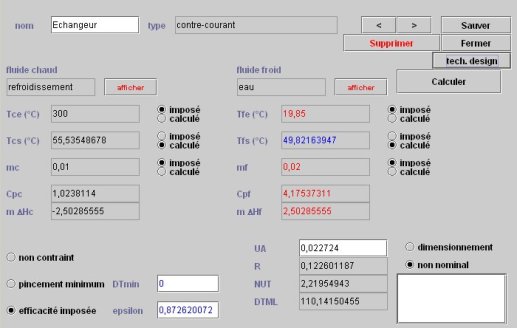
L'erreur que l'on commettrait sur l'estimation de UA en le supposant constant serait ici de 5 % environ.
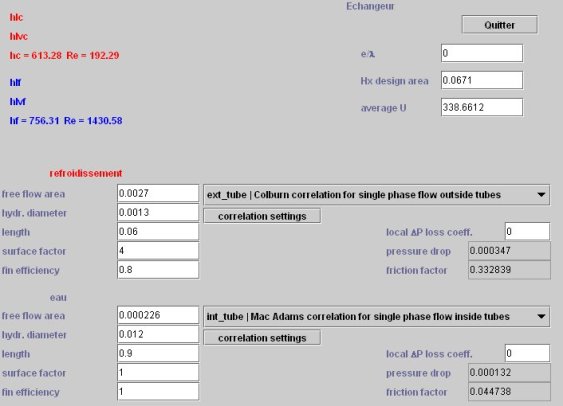
La surface d'échange est bien la même que celle définie lors du dimensionnement.
Dans ce qui précède, nous avons modifié manuellement la valeur de UA dans l'échangeur, l'écran technologique ayant été construit par le pilote générique. Cette manière de faire présente l'avantage qu'elle ne nécessite aucune programmation, mais elle est un peu longue à mettre en pratique dès lors que plusieurs itérations doivent être effectuées. Elle deviendrait donc fastidieuse s'il s'agissait de simuler le comportement en non-nominal de l'échangeur pour une plage de variation large de ses conditions de fonctionnement.
Dans ce cas, il est de loin préférable d'automatiser ces mises à jour en utilisant un pilote spécifique. Un tel exemple sera présenté dans le fil d'Ariane sur les compresseurs volumétriques.