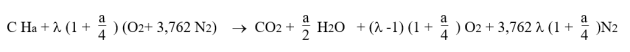Une fois qu'un modèle de Thermoptim est mis au point, ses fichiers de schéma et de projet contiennent toutes les informations permettant sa résolution complète. Il est donc possible de s'en servir pour générer l'ensemble des équations correspondantes, grâce à une fonctionnalité du progiciel en cours de développement.

Cela permet en particulier :

• de conserver une approche système dans la description de l'architecture du modèle, tout en donnant accès à ses équations, pour pouvoir les exploiter dans d'autres environnements et effectuer des traitements complémentaires de ceux du progiciel, par exemple de l'optimisation.

• de garantir la cohérence des jeux d'équations des modèles de grande taille, ce qui peut être difficile en pratique si l'on ne dispose pas d'un outil approprié.

• Thermoptim peut ainsi être utilisé comme pré-processeur de divers solveurs de thermodynamique appliquée, comme Interactive Thermodynamics, EES ou Matlab.

Les conventions utilisées sont les suivantes :

• Les noms des inconnues sont définis par concaténation de leur symbole habituel (T, p, h, s, v...) avec le nom du point ou de la transfo, l'underscore ‘_' servant de liaison. Ainsi, l'enthalpie du point 2 s'écrit h_2. L'intérêt de cette notation est d'une part qu'elle est très claire, et d'autre part qu'elle se transforme en h2 si l'équation est affichée dans des éditeurs utilisant la syntaxe LaTeX. Notez que vous pouvez rajouter des variables et des équations pour les faire analyser par Thermoptim. Dans ce cas, les noms des variables doivent contenir l'underscore pour être pris en compte, et chaque nouvelle équation doit être précédée de la ligne //Equation : ijk, ijk étant son numéro.

• Les débits sont notés ‘m_dot_' suivi du nom de la transfo, par exemple m_dot_condenseur pour le débit qui traverse la transfo ‘condenseur'

• Lorsque des caractères spéciaux ou des espaces sont utilisés dans les noms des éléments de Thermoptim, ils sont purement et simplement supprimés. Par exemple, l'enthalpie du point ‘entrée d'air' s'écrira h_entredair. Rien n'empêche de renommer ensuite cette inconnue si on le souhaite.

• Les fonctions de calcul des propriétés sont générées en deux temps. Elles sont tout d'abord écrites selon le format générique suivant facile à interpréter pour un humain : nomFonction("fluide";T = T_1 ;P = P_1). Les arguments de la fonction sont ainsi clairement identifiables, sans risque de les permuter. Ainsi, le calcul de l'enthalpie de l'eau connaissant sa pression et son entropie s'écrit : calcH_PS("eau";P = p_2;s = s_2)

• Le jeu d'équations ainsi généré peut ensuite être facilement converti au format spécifique de chaque solveur.

• Des commentaires peuvent être ajoutés soit sur une ligne complète, soit après une équation. Ils sont précédés des caractères ‘//', selon la syntaxe utilisée dans un certain nombre de langages de programmation.

• Précisons qu'il n'est pas prévu de fournir les équations pour tous les nombreux paramétrages que permet Thermoptim car, une fois un jeu d'équations établi, il est facile d'en modifier certaines à la main en fonction des objectifs poursuivis. Par exemple, l'équation retenue pour calculer la pression de sortie d'un compresseur peut être le produit de celle d'entrée par le rapport de compression supposé connu. Elle reste valable si la pression est imposée et le rapport de compression calculé. Pour changer le paramétrage, il suffit de changer la valeur connue.

• Une transfo échange ou une chambre de combustion étant en général isobare, nous avons implémenté P_aval = P_amont.

• Dans les transfos points d'entrée, l'état complet est calculé comme une donnée, ainsi que le débit.

• Pour déterminer les débits, on part des transfos à débit imposé ou de celles en aval des nœuds, qui sont tous recalculés, et on propage le débit à celles en aval si la connexion est unique.

• Bien que ce ne soit pas une exigence impérative pour la plupart des solveurs, les équations sont généralement écrites sous la forme « Variable = expression fonction des autres variables »

Pour le moment, la génération formelle d'équations n'est implémentée que pour les composants du noyau de Thermoptim, et cette implémentation reste provisoire. Quelques modifications dans les fichiers générés sont donc à prévoir à l'avenir.

Les équations générées pour une turbine modélisée selon une référence isentropique et à rapport de détente imposé sont ainsi de ce type :

//Process: turbine

//Equation : 23

m_dot_turbine = m_dot_superheater // Upstream process : superheater - Downstream process : turbine

//Equation : 24

s_3 = calcS_PH("water";P = p_3;H = h_3) // Upstream point : 3 - Downstream point : 4

// Comment = Isentropic reference

//Equation : 25

hs_4 = calcH_PS("water";P = p_4;S = s_3) // Downstream point : 4

//Equation : 26

etaT_turbine = 0.9// Isentropic efficiency

//Equation : 27

h_4 = h_3 - etaT_turbine*(h_3 - hs_4) // Upstream point : 3 - Downstream point : 4

//Equation : 28

xl_4 = 0.// Saturated liquid quality

//Equation : 29

Tl_4 = T_4- 0.01// Saturated liquid temperature

//Equation : 30

xv_4 = 1.// Saturated vapor quality

//Equation : 31

Tv_4 = T_4+ 0.01// Saturated vapor temperature

//Equation : 32

hl_4 = calcH_TPx("water";T = Tl_4;P = p_4;X = xl_4)// Saturated liquid enthalpy

//Equation : 33

hv_4 = calcH_TPx("water";T = Tv_4;P = p_4;X = xv_4)// Saturated vapor enthalpy

//Equation : 34

x_4 = (h_4 - hl_4)/(hv_4 - hl_4)// Quality

//Equation : 35

T_4 = calcTsat("water";P = p_4 ;X = x_4) // Downstream point : 4

//Equation : 36

s_4 = calcS_PH("water";P = p_4;H = h_4) // Entropy

// Comment = Given outlet pressure

//Equation : 37

p_4 = 0.0356// Outlet pressure

//Equation : 38

W_dot_turbine = m_dot_turbine*(h_4 - h_3) // DeltaH

L'équation 23 traduit la propagation du débit depuis la transfo amont

L'équation 24 calcule l'entropie du point amont, et la 25 celle de l'enthalpie du point aval correspondant à l'évolution isentropique

L'équation 26 fournit la valeur du rendement isentropique, et la 27 permet de déterminer l'enthalpie réelle du point aval

Les équations 28 à 34 fournissent le titre de sortie turbine

L'équation 35 fournit la température du point aval, et la 36 son entropie.

L'équation 37 donne la pression aval, et la 38 le travail utile.

Thermoptim extrait automatiquement du modèle un premier jeu d'équations commentées que l'on peut qualifier de brutes. Leur nombre est assez élevé, car une transfo en nécessite typiquement plus d'une dizaine : 4 pour l'état de chaque point d'entrée et de sortie (T, p, x, h), 2 pour le débit et l'énergie mise en jeu delta H, plus celles permettant son calcul.

Un modèle même très simple en comporte donc généralement au moins une cinquantaine.

Analyser ce jeu d'équations brutes pour en vérifier la cohérence et les manques éventuels est une tâche qui peut révéler fastidieuse si elle est effectuée à la main.

Des utilitaires permettent de faciliter ce traitement.

La première étape consiste à résoudre les redondances qui peuvent exister entre les équations notamment lorsqu'une variable est calculée de deux façons différentes, ce qui peut arriver en fonction du paramétrage du modèle. L'analyse qui est effectuée considère qu'il y a redondance si une même variable x_y apparaît deux fois à gauche du signe ‘=' : x_y = expression 1, x_y = expression 2.

Ces redondances sont causées par des variantes dans l'interprétation du paramétrage du modèle Thermoptim. Comme le progiciel n'est pas capable de choisir entre les équations concernées, c'est au modélisateur de le faire, d'autant plus que certaines redondances apparentes n'en sont pas de véritables, du fait que certaines variables peuvent devoir être calculées par inversion d'une ou plusieurs équations.

Thermoptim établit la liste des redondances potentielles, et c'est à l'utilisateur de supprimer les équations inutiles en comparant celles qui ont été générées et en retenant celles qu'il désire. Pour cela il lui suffit de double-cliquer sur une ligne de redondance pour ajouter ou supprimer ‘//' devant l'équation, ce qui désactive ou active cette dernière. Le même ‘//' apparaît sur la ligne sélectionnée dans l'écran de droite, pour rappeler qu'elle a été modifiée.

Le choix entre les équations redondantes n'est pas toujours simple. Pour vous aider à choisir, vous pouvez les faire afficher successivement dans l'écran de gauche en double-cliquant sur chacune d'elles, ce qui vous permet d'une part de savoir à quel bloc elle appartient et d'autre part de consulter les commentaires qui l'accompagnent. N'oubliez pas de double-cliquer une deuxième fois pour rétablir l'état précédent de l'équation tant que vous n'avez pas effectué votre sélection définitive.

La seconde étape permet de signaler si une variable du problème n'apparaît jamais à gauche d'une équation, ce qui laisse a priori supposer qu'elle n'est ni initialisée ni calculée à partir d'une des équations. Cela permet de détecter des oublis éventuels dans la définition du problème à résoudre. Un exemple est celui d'un cycle à vapeur simple, dont la température d'entée turbine n'est pas automatiquement considérée par Thermoptim comme une variable imposée. Toutefois, comme pour les redondances, certaines variables n'apparaissent pas explicitement à gauche du signe ‘=' dans les équations, car elles sont calculées par inversion de certaines d'entre elles.

Pour éventuellement réduire la dimension du problème, un algorithme d'ordonnancement des équations restantes a été mis au point et peut être utilisé dans une troisième étape.

Son principe est le suivant.

Il commence par identifier toutes les variables dont Thermoptim considère que la valeur est imposée et dont l'équation générée a la forme « Variable = donnée numérique ».

Par exemple m_dot_condenser = 100 // Set flow

Cela fournit un premier groupe d'équations résolues qui correspond aux données du problème.

Le second groupe est celui dont les équations ne dépendent que des variables du premier groupe.

Par exemple m_dot_feedpump = m_dot_condenser // Flow propagation

Un troisième groupe est celui dont les équations ne dépendent que des variables du premier et du second groupes, et ainsi de suite, l'algorithme opérant de manière récursive.

A la fin reste le groupe des équations à résoudre grâce au solveur, les solutions des autres pouvant être directement obtenues par substitution des variables inconnues par celles déjà calculées.

La présentation de la procédure de réduction de la taille du modèle peut par ailleurs avoir un intérêt didactique.

Bien sûr cet ordonnancement est inutile si le solveur est puissant et utilisé en aveugle.

Comme déjà indiqué, le nombre de paramètres de Thermoptim est très élevé. Il serait difficile de prévoir toutes les équations correspondantes, mais cela ne présenterait de toute manière pas un grand intérêt, étant donné qu'une fois un jeu d'équations validé, il est très simple de le compléter à loisir en fonction des objectifs poursuivis. Seuls donc les principaux paramétrages ont été retenus.

Graphe des dépendances directes

Une fonctionnalité complémentaire a été ajoutée à l'analyse du jeu d'équations généré par Thermoptim.

Lorsqu'une variable fait partie des groupes mis en évidence précédemment, il est possible d'afficher le graphe de ses dépendances directes vis à vis de celles des groupes de rang inférieur. Il suffit pour cela de la sélectionner dans le panneau de gauche de l'écran du processeur d'équations, puis de cliquer sur le bouton "Display dependency graph". L'arbre des dépendances directes est affiché sous deux formes dans deux nouvelles fenêtres, qui permettent de l'exporter au format texte ou carte mentale. L'une des fenêtres affiche simplement le graphe des variables dépendantes, tandis que l'autre affiche en plus les équations qui déterminent cette dépendance, comme le montre la figure ci-dessous.

Notez que l'analyse des équations se fait sur l'ensemble du contenu du panneau de gauche et non pas sur les seules équations générées par Thermoptim. À condition bien sûr qu'il respecte le même format que celles-ci, vous pouvez donc utiliser ces fonctionnalités sur n'importe quel ensemble d'équations.

Notez aussi que ce type de graphe ne peut être établi que pour les seules variables qui peuvent être calculées directement à partir des autres variables des groupes de rang inférieur. Les variables qui ne peuvent être calculées que par la résolution du groupe d'équations non résolues ne peuvent pas être prises en compte.

L'exportation au format Freemind permet de conserver l'arbre de dépendances en tant que carte mentale.

Comme précisé plus haut, les fonctions de calcul des propriétés initialement générées par Thermoptim sont écrites selon le format générique suivant facile à interpréter pour un humain : nomFonction("fluide";T = T_1 ;P = P_1). Les arguments de la fonction sont ainsi clairement identifiables, sans risque de les permuter. Ainsi, le calcul de l'enthalpie de l'eau connaissant sa pression et son entropie s'écrit : calcH_PS("water";P = p_2;s = s_2).

Il est donc nécessaire de les convertir au format spécifique du serveur que l'on désire utiliser. Par exemple, dans Interactive Thermodynamics, cette dernière expression doit être écrite sous la forme h_Ps("water", p_2,s_2), et dans EES enthalpy(Steam;P= p_2;s = s_2).

Il faut aussi bien vérifier le paramétrage des unités dans le solveur. Pour Thermoptim, il s'agit du système SI, les pressions étant exprimées en bar et les températures en °C. L'unité des débits est indiquée avant les équations.

Une fois le jeu équations jugé satisfaisant, il faut donc le convertir dans la syntaxe du solveur particulier qui sera utilisé.

Composition des gaz composés

Les deux solveurs vers lesquels le processus de conversion des équations générées a jusqu'ici été implémenté sont Interactive Thermodynamics et EES.

J'ai été bloqué dans la conversion vers ces deux solveurs du calcul des propriétés des gaz composés de Thermoptim du fait de l'impossibilité à ma connaissance (très partielle certes) de définir un nouveau gaz composé et d'en calculer les propriétés énergétiques. Pour EES, j'ai vu que des solutions existent, mais je ne sais pas comment les automatiser à partir des fichiers de Thermoptim. Pour Interactive Thermodynamics, je n'ai pas vu comment faire.

Cela signifie que les équations des systèmes mettant en jeu de tels fluides ne peuvent pas être entièrement générés par Thermoptim, à l'exception de quelques gaz comme l'air, qui est en fait traité comme un gaz pur. Il faudra que le modélisateur les complète par des fonctions particulières qu'il devra programmer. Afin toutefois de lui faciliter la tâche, la composition de ces gaz composés est indiquée dans le fichier généré sous forme de lignes de commentaires, comme le montre cet exemple :

//GAS COMPOSITIONS

//burnt_gas

//CO2 0.04419006337631066

//H2O 0.03617814048485812

//O2 0.1640556604215191

//N2 0.7433597848138069

//Ar 0.012216350903505186

//air

//N2 0.7555302216468832

//Ar 0.012416359476160373

//O2 0.2320534188769565

//CH4 ` methane

//CH4 ` methane 1.0

Chambres de combustion

La génération des équations correspondant aux chambres de combustion est en particulier un problème complexe du fait du nombre d'options de paramétrage possibles et de la détermination de la composition des gaz brûlés.

Compte tenu de ces difficultés, j'ai opté pour une solution provisoire qui permet de réaliser une combustion dans EES, et donc d'étudier des cycles du type turbines à gaz ou moteurs alternatifs à combustion interne ne mettant en jeu qu'une seule combustion avec de l'air comme comburant et le méthane CH4 comme combustible. Cette solution peut être une première étape avant de développer des modèles plus détaillés des combustions.

La réaction est supposée complète. Son équation est :

Lambda est le facteur d'air, et a est le nombre d'atomes d'hydrogène par atome de carbone. Il vaut en l'occurrence a = 4 pour le méthane.

Lorsque le système étudié comporte une chambre de combustion, le début du fichier généré comporte trois fonctions EES permettant d'estimer :

• le facteur d'air de la combustion en fonction de la température du comburant et de la température de fin de combustion désirée, ainsi que la valeur de a pour un combustible de type CHa

• l'enthalpie des produits de la combustion, en fonction de leur température, du facteur d'air, et de a

• l'entropie des produits de la combustion, en fonction de leur température et de leur pression, du facteur d'air, et de a

Les points amont et aval étant 2 et 3, le bloc d'équations correspondant à une chambre de combustion est du type :

//Process: combustion chamber

// Comment = Calculate lambda simplified model oxidizer air, fuel CH4

//Equation: 28

T_3 = 1065.0// Given value (Celsius)

//Equation: 29

a_combustionchamber = 4// for CH4

//Equation: 30

lambda_combustionchamber = LAMBD(T_2;T_3;a_combustionchamber)// air factor lambda

//Equation: 31

h_3 = h_products(T_3;a_combustionchamber;lambda_combustionchamber)// enthalpy of the reactants

//Equation: 32

hfict_2 = h_products(T_2;a_combustionchamber;lambda_combustionchamber)// enthalpy of a fictitious inlet point for calculating the heat released

//Equation: 33

m_dot_combustionchamber = m_dot_compressor + m_dot_fuel // Upstream process - compressor - Fuel process fuel - Downstream process - combustion chamber

//Equation: 34

//m_dot_turbine = m_dot_combustionchamber //Flow propagation

//Equation: 35

Q_dot_combustionchamber = (h_3 - hfict_2)*m_dot_combustionchamber // DeltaH

//Equation: 36

DeltaHr_combustionchamber = (-(-74850) +(-393520)+a_combustionchamber/2*(-242000))/16 // DeltaHr (kJ/kg) = (-(-74850) +(-393520) + a/2* (-242000))/16 for methane

//Equation: 37

m_dot_fuel = Q_dot_combustionchamber/DeltaHr_combustionchamber // fuel flow rate

// Comment = Isobaric process

//Equation: 38

p_3 = p_2// Isopressure

//Equation: 39

T_fuel = 15.0// Given value (Celsius)

//Equation: 40

p_fuel = 20.0// Given value (bar)

//Equation: 41

h_fuel = calcH_TP("CH4 ` methane";T = T_fuel ;P = p_fuel) // Fuel point - fuel

L'équation 28 fixe la valeur de la température de fin de combustion désirée, la 29 fixe la valeur de a, et la 30 fait appel à la fonction EES donnant lambda.

L'équation 31 calcule l'enthalpie des gaz sortant de la chambre de combustion. Signalons un problème important rencontré à ce niveau : je n'ai pas trouvé la valeur h0 de référence des enthalpies des gaz brûlés à adopter pour qu'elles soient comparables à celles des autres fluides. Il y a donc un écart entre ces deux familles de propriétés. Cela ne pose problème qu'au niveau de la chambre de combustion elle-même.

C'est pour cela que l'enthalpie fictive hfict_2 est introduite dans l'équation 32. Elle permet de connaître la valeur de l'enthapie du point amont calculée avec la composition et les équations du point aval.

L'équation 33 assure la conservation du débit. La 34 a été annulée car rendondante et différente.

L'équation 35 détermine la chaleur libérée lors de la combustion, en utilisant hfict_2 introduite précédemment.

L'équation 36 calcule l'enthalpie de réaction du combustible, et l'équation 37 s'en sert pour déterminer le débit de combustible nécessaire.

L'équation 41 calcule l'enthalpie du combustible. Le nom de son corps devra être modifié pour devenir CH4.

Calculs en aval d'une chambre de combustion

Les calculs en aval de la chambre de combustion demandent des traitements particuliers, du fait que les gaz brûlés ne sont pas reconnus comme un corps. La détermination de leurs propriétés se fait en utilisant deux des trois fonctions EES introduites, qui fournissent l'enthalpie et l'entropie, mais n'inversent pas ces fonctions.

Etant donné que le calcul des propriétés thermodynamiques des gaz brûlés ne peut être effectué avec les fonctions habituelles, il faut remplacer tous les appels à ces dernières pour le corps de Thermoptim qui les représente par leur équivalent défini dans les fonctions EES placées au début du fichier généré. Cela ne pose pas de difficulté particulière pour les calculs liant h et s à T et p, mais est en revanche plus délicat pour ceux reliant directement h et s qui supposent des inversions de ces fonctions.

On est donc amené à légèrement reformuler le problème en fonction de la situation, comme illustré par le calcul d'une turbine en référence polytropique présenté ci-dessous, dont seules les équations de calcul des propriétés demandent à être modifiées. Le point amont est 3 et le point aval 4.

Rappelons que les lignes commençant par // sont des lignes de commentaire dont le solveur ne tient pas compte.

//Process: turbine

// Comment = Polytropic coefficient: k = -Math,log(aval,p/amont,p)/Math,log(aval,V/amont,V)

//Equation: 24

//h_4 = enthalpy(burnt gases;P = p_4;S = s_4) // Enthalpy

h_4 = h_products(T_4;a_combustionchamber;lambda_combustionchamber)// enthalpy of the reactants

//Equation: 25

//T_4 = temperature(burnt gases;H = h_4) // Downstream point - 4

s_4 = s_products(T_4;p_4;a_combustionchamber;lambda_combustionchamber)// enthalpy of the reactants

Les équations 24 et 25 sont remplacées de la manière suivante : calcul de h_4 en fonction de T_4 (inconnue), fournie par l'inversion par le solveur de l'équation donnant s_4 (connue) en fonction de T_4.

Comme on le voit, il faut dans ce cas reformuler légèrement le problème.

Pour une détente isentropique, voici un exemple un peu plus complexe de reformulation.

//Equation: 18

//s_3 = entropy(burnt gases;P = p_3;H = h_3) // Upstream point - 3 - Downstream point - 4

s_3 = s_products(T_3;P_3;a_combustionchamber;lambda_combustionchamber)

// Comment = Isentropic reference

//Equation: 19

//hs_4 = enthalpy(burnt gases;P = p_4;S = s_3) // Downstream point - 4

hs_4 = h_products(Tis;a_combustionchamber;lambda_combustionchamber)

s_3 = s_products(Tis;P_4;a_combustionchamber;lambda_combustionchamber)

//Equation: 20

etaT_turbine = 0,85// Isentropic efficiency

//Equation: 21

h_4 = h_3 - etaT_turbine*(h_3 - hs_4) // Upstream point - 3 - Downstream point - 4

//Equation: 22

//T_4 = temperature(burnt gases;H = h_4) // Downstream point - 4

h_4 = h_products(T_4;a_combustionchamber;lambda_combustionchamber)

//Equation: 23

//s_4 = entropy(burnt gases;P = p_4;H = h_4) // Entropy

s4 = s_products(T_4;P_4;a_combustionchamber;lambda_combustionchamber)

L'équation 18 est une simple reformulation de celle générée.

Pour résoudre l'équation 19, on introduit la température isentropique Tis, qui est déterminée à partir de la fonction donnant l'enthalpie connue, et l'équation donnant l'enthalpie à partir de Tis fournit l'enthalpie isentropique.

Les équations 22 et 23 sont de simples reformulations de celles générées.

Trois exemples commentés sont fournis dans ces pages, avec les fichiers d'équations correspondants, ainsi que d'autres non commentés.

• Cycle de centrale à vapeur

• Cycle de réfrigération

• Cycle de turbine à gaz

• Cycles combinés à un et deux niveaux de pression