Il s'agit d'un cycle très simple dont le synoptique est donné ci-dessous :

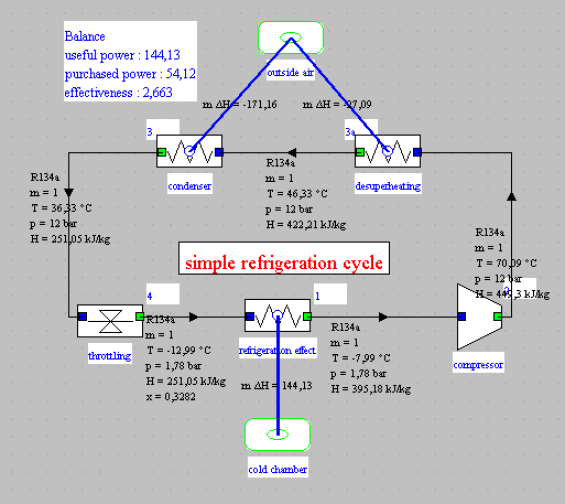
Les fichiers de schéma et de projet sont donnés ci-dessous. Attention, ils nécessitent d'utiliser Thermoptim en version anglaise, c'est-à-dire avec le fichier inth2.zip de cette langue.

Il y en a 47. Elles sont données dans ce fichier.

Les redondances identifiées sont les suivantes :

Redundancy for x_4:

# 1 x_4 = (h_3 - hl_4)/(hv_4 - hl_4), equation: 22

# 2 x_4 = 0.328174791, equation: 41

Redundancy for T_4:

# 1 T_4 = calcTsat("R134a";P = p_4 ;X = x_4), equation: 23

# 2 T_4 = calcTsat("R134a";P = p_4;X = x_4)+dTsat_4, equation: 43

Redundancy for h_4:

# 1 h_4 = calcH_TPx("R134a";T = T_4;P = p_4;X = x_4), equation: 24

# 2 h_4 = calcH_TPx("R134a";T = T_4;P = p_4;X = x_4), equation: 44

Redundancy for p_4:

# 1 p_4 = 1.78, equation: 15

# 2 p_4 = 1.78, equation: 40

Dans l'équation 22, x_4 est calculé, et dans l'équation 41 sa valeur est donnée. La seconde équation doit donc être supprimée. Cette redondance provient de ce qu'il s'agit d'un point à température de saturation imposée et que donc il est a priori considéré comme une donnée du problème, alors qu'il doit être recalculé si les paramètres changent.

La redondance sur h_4 est de même nature. Il faut conserver l'équation 24.

Les redondances sur h_4 et p_4 correspondent à des équations en double. Il faut à chaque fois en supprimer une.

La seule variable non initialisée est m_dot_throttling. Cela provient de ce qu'aucune des transfos n'est à débit imposé. Il faudra donc compléter le jeu d'équations en initialisant m_dot_throttling à la valeur du débit.

Une fois l'équation manquante rajoutée, l'analyse des équations peut être recommencée. Elle permet de mettre en évidence les différents groupes d'équations qui peuvent être résolues simplement.

Groupe 1

Group 1 (16 Variables) : [dTsat_1, p_2, x_3a, dTsat_3, m_dot_throttling, p_1, dTsat_4, p_4, p_3, p_3a, xv_4, x_1, x_3, xl_4, etaT_compressor, dTsat_3a]

Group 1 (Equations):

etaT_compressor = 0.75

p_2 = 12.0

xl_4 = 0.

xv_4 = 1.

p_1 = 1.78

x_1 = 1.0

dTsat_1 = 5.0

p_3a = 12.0

x_3a = 1.0

dTsat_3a = 0.0

p_3 = 12.0

x_3 = 0.0

dTsat_3 = -10.0

p_4 = 1.78

dTsat_4 = 0.0

m_dot_throttling=1

On retrouve bien ici toutes les équations fournissant les données du problème, y compris m_dot_throttling.

Groupe 2

Group 2 (4 Variables) : [T_1, T_3, m_dot_refrigerationeffect, T_3a]

Group 2 (Equations):

m_dot_refrigerationeffect = m_dot_throttling

T_1 = calcTsat("R134a";P = p_1;X = x_1)+dTsat_1

T_3a = calcTsat("R134a";P = p_3a;X = x_3a)+dTsat_3a

T_3 = calcTsat("R134a";P = p_3;X = x_3)+dTsat_3

Ce deuxième groupe correspond à des équations permettant de calculer les nouvelles variables par simple substitution de celles du premier groupe.

Groupe 3

Group 3 (4 Variables) : [h_3a, h_1, h_3, m_dot_compressor]

Group 3 (Equations):

m_dot_compressor = m_dot_refrigerationeffect

h_1 = calcH_TPx("R134a";T = T_1;P = p_1;X = x_1)

h_3a = calcH_TPx("R134a";T = T_3a;P = p_3a;X = x_3a)

h_3 = calcH_TPx("R134a";T = T_3;P = p_3;X = x_3)

Ce troisième groupe correspond à des équations permettant de calculer les nouvelles variables par simple substitution de celles du premier et du deuxième groupes. Ici la propagation du débit dans le circuit.

Le processus se répète dans les groupes suivants.

On obtient in fine comme équations non résolues la liste suivante :

Unresolved Equations: 10

Q_dot_refrigerationeffect = m_dot_refrigerationeffect*(h_1 - h_4)

Tl_4 = T_4- 0.01

Tv_4 = T_4+ 0.01

hl_4 = calcH_TPx("R134a";T = Tl_4;P = p_4;X = xl_4)

hv_4 = calcH_TPx("R134a";T = Tv_4;P = p_4;X = xv_4)

x_4 = (h_3 - hl_4)/(hv_4 - hl_4)

T_4 = calcTsat("R134a";P = p_4 ;X = x_4)

h_4 = calcH_TPx("R134a";T = T_4;P = p_4;X = x_4)

useful_Energy = Q_dot_refrigerationeffect

eta_global = abs(useful_Energy/purchased_Energy)

Ce sont celles qui soit dépendent des propriétés du fluide, soit ne peuvent pas être directement résolues.

Les 10 variables manquantes sont aussi identifiées.

Interactive Thermodynamics est un solveur mis à disposition par MM. Moran, Shapiro et Mmes Boettner et Bailey comme complément de leur livre « Fundamentals of Engineering Thermodynamics, 8th Edition » qui peut être téléchargé librement.

La conversion permet d'obtenir un fichier qui peut être traité par le solveur.

Les équations de calcul des propriétés de fluide converties à ce format sont données ci-dessous, les autres restant inchangées :

//Equation: 8

s_1 = s_Ph("R134a",p_1,h_1) // Upstream point - 1 - Downstream point - 2

//Equation: 9

hs_2 = h_Ps("R134a",p_2,s_1) // Downstream point - 2

//Equation: 12

T_2 = T_Ph("R134a",p_2,h_2) // Downstream point - 2

//Equation: 20

hl_4 = hsat_Px("R134a",p_4,xl_4)// Saturated liquid enthalpy

//Equation: 21

hv_4 = hsat_Px("R134a",p_4,xv_4)// Saturated vapor enthalpy

//Equation: 23

T_4 = Tsat_P("R134a",p_4) // Downstream point - 4

//Equation: 24

h_4 = hsat_Px("R134a",p_4,x_4) // Enthalpy

//Equation: 28

T_1 = Tsat_P("R134a",p_1)+dTsat_1// set Tsat (Celsius)

//Equation: 29

h_1 = hsat_Px("R134a",p_1,x_1)// Enthalpy

//Equation: 33

T_3a = Tsat_P("R134a",p_3a)+dTsat_3a// set Tsat (Celsius)

//Equation: 34

h_3a = hsat_Px("R134a",p_3a,x_3a)// Enthalpy

//Equation: 38

T_3 = Tsat_P("R134a",p_3)+dTsat_3// set Tsat (Celsius)

//Equation: 39

h_3 = hsat_Px("R134a",p_3,x_3)// Enthalpy

//Equation: 43

T_4 = Tsat_P("R134a",p_4)+dTsat_4// set Tsat (Celsius)

//Equation: 44

//h_4 = hsat_Px("R134a",p_4,x_4)// Enthalpy

Le fichier complet pouvant être résolu dans Interactive Thermodynamics est fourni ci-dessous.

EES est un solveur développé par f-Chart, qui nécessite de disposer d'une licence.

La conversion permet d'obtenir un fichier qui peut être traité par le solveur.

Les équations de calcul des propriétés de fluide converties à ce format sont données ci-dessous, les autres restant inchangées :

//Equation: 8

s_1 = entropy(R134a;P = p_1;H = h_1) // Upstream point - 1 - Downstream point - 2

//Equation: 9

hs_2 = enthalpy(R134a;P = p_2;S = s_1) // Downstream point - 2

//Equation: 11

h_2 = h_1 + (hs_2 - h_1)/etaT_compressor // Upstream point - 1 - Downstream point - 2

//Equation: 12

T_2 = temperature(R134a;P = p_2;H = h_2) // Downstream point - 2

//Equation: 20

hl_4 = enthalpy(R134a;P = p_4;X = xl_4)// Saturated liquid enthalpy

//Equation: 21

hv_4 = enthalpy(R134a;P = p_4;X = xv_4)// Saturated vapor enthalpy

//Equation: 24

h_4 = enthalpy(R134a;P = p_4;X = x_4) // Enthalpy

T_1 = t_sat(R134a;P = p_1)+dTsat_1// set Tsat (Celsius)

//Equation: 29

h_1 = enthalpy(R134a;P = p_1;X = x_1)// Enthalpy

//Equation: 33

T_3a = t_sat(R134a;P = p_3a)+dTsat_3a// set Tsat (Celsius)

//Equation: 34

h_3a = enthalpy(R134a;P = p_3a;X = x_3a)// Enthalpy

//Equation: 38

T_3 = t_sat(R134a;P = p_3)+dTsat_3// set Tsat (Celsius)

//Equation: 39

h_3 = enthalpy(R134a;P = p_3;X = x_3)// Enthalpy

Le fichier complet pouvant être résolu dans EES est fourni ci-dessous.