Les expressions permettant de calculer les échanges d'énergie mécanique et thermique d'une masse fluide avec son environnement ont été établies dans une autre page.

Pour présenter le premier principe de la thermodynamique, nous commencerons par son expression pour les systèmes fermés, bien connue de tous, et nous la généraliserons pour les systèmes ouverts.

Le premier principe, connu aussi sous le nom de principe de l'équivalence ou principe de la conservation de l'énergie, exprime que l'énergie contenue dans un système isolé ou qui évolue selon un cycle fermé reste constante, quelles que soient les transformations qu'il subit. Les différentes formes que peut prendre l'énergie d'un système : énergie mécanique, énergie calorifique, énergie potentielle, énergie cinétique… sont toutes équivalentes entre elles au sens du premier principe.

A tout système physique fermé est attaché un scalaire U, fonction des seules variables d'état, et tel qu'on a en toute transformation réelle :

ΔU + ΔK = W + Q (1 )

K étant l'énergie cinétique du système, W le travail des forces externes, exprimé pour la masse totale du système et donné par la relation : W = WA + Wv, et Q la quantité de chaleur échangée par le système avec l'extérieur pendant la transformation considérée.

U est une grandeur extensive^[2] appelée l'énergie interne du système, U + K est parfois appelée son énergie totale. Pour une phase^[1] de masse m, U = m u, u étant l'énergie interne massique.

Rappelons que les variables d'état qui définissent, dans le cas le plus général, un système physique, appartiennent à quatre grandes catégories, dont seules les deux premières seront à considérer dans la plupart des applications que nous aurons à traiter ; la troisième ne sera utilisée que pour les mélanges de fluides et les réactions de combustion ; quant à la quatrième, elle n'interviendra pas ici :

• les variables mécaniques, de position ou de déformation ;

• la température^[3] ;

• les variables chimiques ;

• les variables électriques.

On notera que de nombreux auteurs distinguent dans l'expression du premier principe le travail de la pesanteur (Wv) et celui des forces de pression (WA), et l'expriment donc sous la forme équivalente :

ΔU + ΔK + mg Δz = WA + Q

Pour un volume de contrôle infiniment petit, l'équation (1) devient :

dU + dK = dW + δQ (2)

Physiquement, le premier principe découle de la mise en évidence expérimentale du fait que, quelles que soient les transformations subies par un système donné, la somme W + Q ne dépend que de l'état initial et de l'état final. Il en résulte donc que W + Q est une fonction d'état^[4] du système.

Mathématiquement, le premier principe indique que, alors que δW et δQ ne sont pas des différentielles exactes, leur somme en est une, et qu'elle est égale à la somme des variations de l'énergie cinétique et d'une fonction d'état^[4] , l'énergie interne.

Pour une phase^[1] fluide simple, l'état physique du système, exprimé en grandeurs massiques, est caractérisé par les variables P, v, T, reliées entre elles par l'équation d'état. u est donc fonction de ces variables, ou plus précisément de deux d'entre elles.

Appliquons le premier principe à une transformation réversible^[5] infiniment petite du fluide, en négligeant l'action de la pesanteur. Au cours d'une telle transformation, l'énergie cinétique reste constamment nulle, ce qui implique dK = 0. Par ailleurs δW = - Pdv, et δQ s'exprime sous la forme :  

δQ = du + Pdv (3)

Par identification avec l'équation calorimétrique, on retrouve bien :

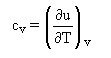
qui est souvent utilisée comme définition de cv

L'équation précédente montre que, pour un échauffement à volume constant, sans frottements mécaniques, la chaleur échangée avec l'extérieur est égale à la variation d'énergie interne du fluide :

Q= u2 - u1

Cette relation est à la base des déterminations calorimétriques de u.

Les opérations industrielles se déroulent généralement en continu, chaque composant (turbine, pompe, vanne...) recevant et évacuant de la matière en permanence. Le calcul de ces appareils doit donc être fait en système ouvert^[6][6], et l’expression précédente, valable uniquement en système fermé^[6], doit être généralisée.

Le principe du raisonnement consiste à suivre l'évolution d'un volume de contrôle fermé, et à calculer le travail des forces externes sur l'ensemble de ses frontières, en distinguant les sections de passage des fluides, les parois fixes, qui bien évidemment ne produisent ni ne reçoivent aucun travail, et les parois mobiles, au niveau desquelles s'exerce un certain travail que l'on appelle "travail utile^[7]".

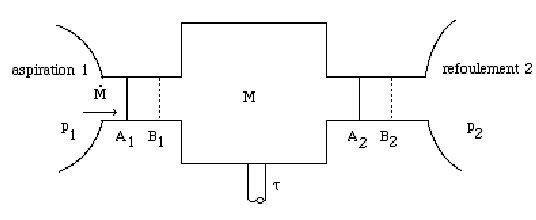
Dans le cas le plus fréquent (figure ci-dessus), on peut supposer que le composant fonctionne entre deux enceintes de grandes dimensions, où le fluide est en équilibre^[8]. Les états amont (1) et aval (2) sont définis par leurs pressions et leurs températures supposées uniformes malgré les prélèvements et les apports dus à l'aspiration et au refoulement. Par exemple, un compresseur de turbine à gaz aspire dans l'atmosphère et refoule dans la chambre de combustion où règne une pression sensiblement uniforme.

Dans son passage de (1) à (2), chaque unité de masse de fluide reçoit, de la part des parois mobiles, le travail utile^[7] , dont la connaissance est fondamentale, puisque son produit par le débit-masse donne la puissance mise en jeu (aux pertes mécaniques près dans les paliers et organes de transmission).

On peut facilement démontrer que, par unité de masse, un composant réalisant une transformation quelconque fournit un travail algébriquement égal au travail WA des forces de pression calculées en système fermé^[6], augmenté du travail de transvasement, c'est-à-dire de la variation du produit Pv :

= WA + P2v2 - P1v1 = WA + Δ(Pv)

On remarquera que, dans la relation précédente, nous n'avons fait aucune hypothèse restrictive sur la nature des transformations dans la machine proprement dite. Nous avons simplement admis que la pression était uniforme et constante dans la suite des temps à l'entrée et à la sortie de la machine. La relation obtenue s'applique donc sous cette seule condition, quelles que soient les transformations intermédiaires, qu'elles soient réversibles ou non.

Cas particulier d'une transformation réversible

Si la transformation est réversible,

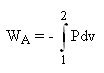
= WA+ P2v2 - P1v1

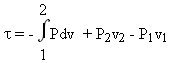
On reconnaît l'expression de l'intégration par partie, d'où :

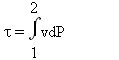
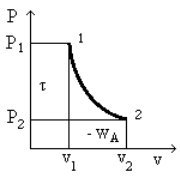
L'ensemble de ces relations est susceptible d'une représentation graphique dans le diagramme de Clapeyron, qui correspond au plan (v,P), v en abscisse, P en ordonnée (figure ci-dessus). L'aire située entre la courbe 1-2 représentant la transformation et l'axe des abscisses est égale à l'opposé du travail des forces extérieures WA, tandis  que l'aire comprise entre cette courbe et l'axe des ordonnées est égale au travail utile^[7] .

On notera que ces surfaces dépendent du tracé de la courbe 1- 2 et donc que la seule connaissance des états initial et final ne suffit pas à déterminer WA et .

Mathématiquement, ce fait important résulte de ce que les expressions différentielles -Pdv et vdP ne sont pas des différentielles exactes. Physiquement, il s'explique par l'intervention d'une forme d'énergie autre que le travail mécanique, à savoir l'énergie thermique.

Si deux transformations réversibles différentes partant du même état initial 1 et aboutissant au même état final 2 ne correspondent pas au même travail utile^[7], cela tient à ce que le fluide n'échange pas la même quantité de chaleur avec l'extérieur au cours de ces deux transformations.

C'est pour cette raison que nous notons les formes différentielles avec un petit δ (δWA, δ ) et les différentielles exactes par d.

Reprenons l'équation (1) et exprimons-la en fonction de et non plus de W, pour la masse totale du système.

Il vient :

ΔU + ΔK = W + Q = WA + Wv + Q = - Δ(PV) - mgΔz + Q

qui peut s'écrire :

Δ(U + PV) + ΔK + mg Δz = + Q

Appelons enthalpie la fonction d'état^[4] H = U + PV et enthalpie massique la fonction h = u + Pv.

L'expression enthalpique du premier principe s'écrit donc en variables massiques (on notera que K, et Q sont dorénavant exprimés en grandeurs massiques) :

Δh + ΔK + gΔz = + Q (6)

Pour un volume de contrôle infiniment petit, cette équation devient :

dh + dK + gdz = δ + δQ (7)

En transposant le raisonnement précédent, on trouve que l'équation calorimétrique se met sous la forme :

δQ = dh - vdP (8)

et que :

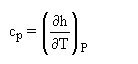
qui est souvent utilisée comme définition de cp.

Cette notion de travail utile est loin d'être triviale. Sur le plan pratique cependant, elle ne pose pas de problème particulier : dans toutes les compressions et détentes en système ouvert^[6][6], c'est le travail utile qui devra être considéré dans les calculs.

Le terme anglais pour désigner le travail utile est "shaft work".