Deuxième principe
DEUXIÈME PRINCIPE DE LA THERMODYNAMIQUE
Le premier principe postule l'équivalence des différentes formes d'énergie, mais il ne permet pas de prendre en compte un fait expérimental essentiel, qui est que, lorsqu'un système interagit avec son environnement, les transformations d'énergie qu'il subit ne peuvent s'effectuer que dans un sens privilégié, que l'on ne peut inverser sans modifier qualitativement le système.
Ainsi, la chaleur s'écoule naturellement d'un corps à température[1] élevée vers un corps à basse température, mais l'inverse ne peut être réalisé qu'en utilisant une machine thermique complexe appelée frigopompe ou pompe à chaleur, ou bien en utilisant un composant électrique à effet Peltier.
Le deuxième principe vient compléter le premier, en introduisant une fonction appelée l'entropie, qui permet de caractériser quantitativement les effets des irréversibilités qui prennent place dans un système et qui expliquent les phénomènes dont nous venons de parler.
Une présentation rigoureuse et générale du deuxième principe demande des développements significatifs du fait d'une part des précautions qu'il faut prendre dans l'écriture des postulats et l'explication de leurs liens avec l'expérience, et d'autre part des démonstrations qu'il faut effectuer.
Compte tenu des objectifs de ce portail, elle ne se justifie pas ici, d'autant plus qu'au plan pratique, pour les calculs de thermodynamique appliquée que nous envisageons, l'intérêt principal que présente le deuxième principe peut se résumer en deux points :
d'une part l'entropie est comme nous le montrerons la fonction d'état[2] la plus directement liée à la chaleur Q échangée avec l'extérieur (par la relation simple δQ = T ds). Elle intervient donc formellement dans de nombreuses équations gouvernant le fonctionnement des composants énergétiques ;
d'autre part la génération d'entropie permet à elle seule de quantifier toutes les irréversibilités qui prennent place dans ces composants et à leur frontière, ce qui est fondamental.
C'est pourquoi nous avons retenu la présentation ci-dessous, suffisante pour notre propos, et qui présente l'avantage d'être assez courte à énoncer et simple à comprendre.
DÉFINITION DE L'ENTROPIE
A toute phase[3] sont attachées deux grandeurs T et s, dénommées respectivement température[1] thermodynamique et entropie, jouissant des propriétés suivantes :
T est une fonction de la température[1] seule, indépendante du système considéré
s est une fonction des variables d'état du système
dans toute transformation élémentaire mettant en jeu un échange de chaleur dQ avec l'extérieur, on a δQ <= Tds, l'égalité étant vérifiée si et seulement si la transformation est parfaite (non irréversible).
ds = δQ/T+ dis (1)
dis, positif ou nul, est appelée "génération d'entropie".
(1) peut encore s'écrire :
δQ + δ
 = Tds (2)
= Tds (2)
δ
 s'appelle le "travail non compensé" ou la "chaleur non compensée". Il est positif pour une transformation irréversible[4], et nul dans le cas contraire.
s'appelle le "travail non compensé" ou la "chaleur non compensée". Il est positif pour une transformation irréversible[4], et nul dans le cas contraire.
L'introduction ex abrupto de l'entropie peut surprendre et apparaître arbitraire. Pour essayer de l'expliquer de manière plus progressive, nous allons étudier le cas des gaz parfaits, dont l'équation d'état s'écrit :
P v = r T
r étant une constante dépendant du gaz (r = 287 J/kg pour l'air), v étant le volume massique, et T la température exprimée en degrés Kelvin.
Cette équation résulte des lois :
de Gay-Lussac ( P/T = Cste à volume donné),
de Mariotte (Pv = Cste à température donnée).
Les propriétés thermiques des gaz parfaits résultent des lois de Joule, qui peuvent être énoncées sous la forme suivante :
première loi : l'énergie interne d'un gaz parfait ne dépend que de sa température.
deuxième loi : la capacité thermique massique à volume constant cv est une constante.
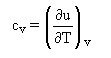
cv = du/dT
Comme δQ = du + Pdv, on a :
δQ = cv dT + Pdv
En remplaçant P par sa valeur issue de l'équation d'état, il vient :
δQ = cv dT + r T dv/v
Posons ds =δQ/T = cv dT/T + r dv/v
Sous cette forme, on s'aperçoit immédiatement que 1/T est un facteur intégrant, et que c'est manifestement le plus simple possible. Rappelons qu'en multipliant tous les termes d'une forme différentielle dy par un facteur intégrant I, on la transforme en une différentielle exacte.
ds étant une différentielle exacte, il vient :
s = cv ln(T) + r ln(v) + Cste.
Les notions de température thermodynamique et d'entropie sont ainsi introduites de manière naturelle, l’entropie étant la fonction d’état la plus proche de la chaleur. Rien ne prouve cependant dans cette approche que ces notions garderont leur pertinence pour des gaz non parfaits. L'avantage de l'approche axiomatique du début de cette section est qu'elle permet ensuite de retrouver les propriétés des gaz parfaits comme cas particulier de la théorie générale.
IRRÉVERSIBILITÉS
Les irréversibilités que l'on rencontre dans les installations énergétiques que nous considérons dans ce portail, à l'exception de celles qui prennent place dans les réactions de combustion, peuvent être regroupées en deux grandes classes que nous présenterons succinctement :
les irréversibilités mécaniques dues à la viscosité ;
les irréversibilités par hétérogénéité de température.
Les relations
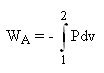
permettent de calculer l'énergie mécanique reçue par un système ouvert[5] ou fermé en l'absence d'irréversibilités. Lorsque les transformations ne sont plus réversibles, elles ne sont plus valables, et, dans le cas général, on ne dispose pas de relations différentielles aussi simples pour déterminer les échanges d'énergie mécaniques mis en jeu.
Le premier principe de la thermodynamique permet cependant de résoudre cette difficulté, comme nous allons le voir maintenant.
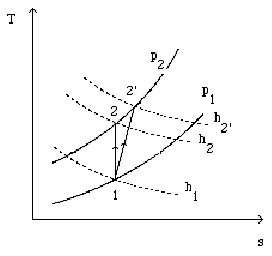
Considérons un système ouvert[5] subissant une compression adiabatique irréversible, de l'état 1 à l'état 2', et tel que les variations d'énergie cinétique puissent être négligées (figure ci-dessus). Compte tenu du premier principe, comme Q = 0, on a :
 = h2' - h1
= h2' - h1
h étant une fonction d'état[6] , on est en droit de décomposer la variation d'enthalpie dans la compression irréversible comme la succession des deux variations correspondant aux transformations suivantes :
une compression isentropique de 1 en 2 mettant en jeu le travail
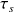
un échauffement isobare fictif de 2 en 2' de valeur
 correspondant aux irréversibilités
correspondant aux irréversibilités
h2' - h1= h2' – h2+ h2 – h1 =
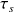 +
+

En conclusion
 = δ
= δ
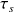 +
+
 (3)
(3)
δ
 = vdP + δ
= vdP + δ
 (4)
(4)
Le raisonnement se transpose facilement à une détente irréversible, ainsi qu'aux systèmes fermés, pour lesquels on a :
W = Ws +
 (5)
(5)
δW = - Pdv + δ
 (6)
(6)
Ces relations se généralisent pour le cas où les énergies cinétiques ou les forces massiques doivent être prises en compte :
δ
 + δQ= dh + dK
+ δQ= dh + dK
δ
 = dh + dK - δQ
= dh + dK - δQ
δ
 = dh + dK – (dh – vdP) = vdP + dK
= dh + dK – (dh – vdP) = vdP + dK
Si les énergies cinétiques ne sont pas négligeables : δ
 = vdP + dK
= vdP + dK
Si les forces massiques ne sont pas négligeables : δ
 = vdP + dK + gdz
= vdP + dK + gdz
En présence d'irréversibilités : δ
 = vdP + dK + gdz + δ
= vdP + dK + gdz + δ
 (7)
(7)
Ces irréversibilités internes donnent lieu à une augmentation d'entropie, qui peut être calculée par application du deuxième principe.
Irréversibilités par hétérogénéité de température
La deuxième grande source d'irréversibilités que l'on rencontre dans les systèmes énergétiques considérés ici provient de la différence de température qui doit en pratique exister entre deux corps lorsqu'ils échangent de la chaleur. En effet, pour des raisons tant techniques qu'économiques, les surfaces d'échange entre ces corps sont nécessairement de dimension finie. Il est alors possible de montrer que l'échange de chaleur s'accompagne d'une augmentation d'entropie à la frontière entre les deux corps (à températures T
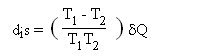
δQ étant la chaleur absorbée par le corps 2. Ces irréversibilités sont souvent qualifiées d'externes, car elles prennent place à la frontière du système considéré.
