Les composants des machines thermiques sont parcourus par des fluides qui sont le plus souvent à l'état gazeux ou liquide. Au cours des transformations qu'ils y subissent, ces fluides échangent de l'énergie avec l'extérieur ou entre eux sous deux formes :

• mécanique, notée traditionnellement W

• thermique notée Q.

Compte tenu de leur importance pratique, nous commencerons par étudier ces échanges d'énergie.

Conformément à notre parti pris de privilégier un exposé aussi simple que possible des bases de la thermodynamique, nous nous limiterons dans ce qui suit à des systèmes en régime permanent, car, même si les résultats que nous établirons se généralisent assez facilement, il est alors nécessaire d'adopter un formalisme plus lourd si l'on veut être rigoureux.

Considérons un système fermé^[1] monophasé. Les forces extérieures qui s'exercent sur lui se limitent généralement

• d'une part à l'action de la pesanteur sur la masse fluide,

• d'autre part aux pressions qui s'exercent sur ses frontières

Dans les machines thermiques, le travail de la pesanteur est dans la majorité des cas négligeable devant celui des actions dites "de contact".

Pour fixer les idées, le travail fourni par une masse de 1 kg d'eau tombant d'une hauteur de 100 m est égal à 980 J, alors que celui de la même masse de vapeur d'eau détendue de manière isentropique de 100 bars et 500 °C à 1 bar est égal à 983 kJ, soit 1000 fois plus importante.

En conséquence, dans les machines thermiques, le travail des forces massiques sera le plus souvent négligeable devant celui de la pression.

Considérons un fluide au repos (figure ci-dessous), donc à pression uniforme P, enfermé dans un cylindre dont toutes les parois sont fixes excepté un piston susceptible de se déplacer dans une direction. Exerçons maintenant une force F sur ce piston, afin de le déplacer suffisamment lentement (pour qu'à tout moment le système puisse être assimilé à une phase ^[2]).

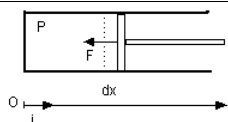
Donnons-nous un axe (O, i) orienté depuis le fond du cylindre (x=0 et V=0). La force étant exercée par l'extérieur sur le système,  F = - ||F|| i

Appelons A la section du piston, et dx le déplacement effectué.

On a bien évidemment ||F|| = P A, et le travail m dWA reçu par la masse m de fluide est :

m dWA  = - ||F|| dx = - P A dx = - P dV.

dV étant la variation de volume de la masse, égale à mdv, et :

dWA = - Pdv

S'il s'agit d'une compression, la variation de volume est négative et le travail reçu est positif. Nous notons d'un indice A ce travail.

Cette expression se généralise sans peine à un système fermé de forme quelconque. Elle n'est valable que si le système reste en équilibre statique^[3], c’est-à-dire si les hypothèses ci-dessous sont vérifiées :

• la pression reste uniforme dans le système ;

• le fluide reste au repos.

On remarquera que la formule (1) implique que le travail reçu par le système est positif, et que le travail qu'il cède est négatif. Par convention, on généralise ce résultat en comptant positivement l'énergie reçue par un système, et négativement celle qu'il fournit à l'extérieur.

Au cours d'une transformation réversible^[4] faisant passer une phase^[2] fermée d'un état^[5] 1 à un état 2, le travail massique des actions de contact a donc pour valeur :

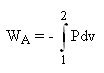
Si le travail de la pesanteur n'est pas négligeable, on peut facilement montrer qu'il s'exprime sous la forme :

dWv = -g δz (3)

g > 0 étant l'accélération de la pesanteur, et z l'altitude du point, comptée positivement vers le haut. Nous notons d'un indice v ce travail.

On a donc :

W = WA + WV (4)

Soit une masse fluide simple, à l'intérieur de laquelle il ne se produit pas de frottements. Soit δQ la quantité de chaleur échangée avec l'extérieur et reçue par l'unité de masse de ce fluide, au cours d'une transformation infiniment petite.

Un fait expérimental essentiel, base de la thermodynamique des fluides compressibles, est que δQ est une forme différentielle de l'état^[5] de cette masse fluide, appelée équation calorimétrique.

A titre d'exemple, dans le cas d'un système monovariant (équilibre ^[3]entre phase^[2]s lors d'un changement d'état), l'équation calorimétrique ne dépend que du titre x, rapport de la masse de vapeur à la masse totale (vapeur + liquide) dans le cas d'une vaporisation ou d'une condensation :

δQ = L dx

L étant l'enthalpie de changement d'état.

Plus généralement, l'équation calorimétrique qui relie δQ aux variables d'état du fluide simple (bivariant) peut prendre les trois formes canoniques équivalentes entre elles bien connues :

• δQ = cp dT + h dP

• δQ = cv dT + l dv (5)

• δQ = m dP + l dv

Les coefficients cp, cv, h, l, m et l sont dits coefficients calorimétriques d'équilibre du fluide (on notera que h n'est pas l'enthalpie).

Ils sont reliés par des relations différentielles que l'on peut obtenir sans difficulté notable mais qui ne présentent pas d'intérêt particulier pour nous. Il suffit de savoir que les propriétés calorimétriques d'un fluide sont déterminées par la connaissance de deux de ces six coefficients.

Par la suite, nous nous servirons uniquement des coefficients cp et cv, qui sont appelés respectivement capacité thermique massique à pression constante, et capacité thermique massique à volume constant, dont l'anciennne appellation était "chaleur massique" (ou spécifique).

Pour un solide ou un liquide, cp = cv, et δQ = c dT

Pour un gaz idéal, h = l = 0, et, selon que l'on a affaire à un système ouvert^[1] ou fermé, δQ = cp dT ou δQ = cv dT. Pour un gaz réel, il faut utiliser une des formes canoniques ci-dessus.

Les équations précédentes ne sont cependant valables que si certaines conditions sont respectées :

• tout d'abord, la masse fluide doit être parfaitement homogène, c'est-à-dire assimilable à une phase^[2] ;

• ensuite, on a supposé qu'il n'y avait pas d'irréversibilité à l'intérieur ou aux limites de la masse fluide.

S'il y en a, la relation devient : 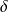 Q < cp dT + h dP

On posera alors : 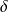 Q = cp dT + h dP - 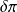(6)

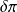, terme essentiellement positif, a une signification physique très simple : c'est la chaleur dégagée par les frottements mécaniques au sein du fluide. Bien qu'elle en diffère profondément, elle produit le même effet qu'une chaleur reçue de l'extérieur. Son sens sera précisé lors de la présentation du deuxième principe de la thermodynamique .

Par convention donc, nous noterons Q la chaleur échangée avec l'extérieur, comptée positivement si elle est reçue par le système, et 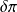la chaleur dissipée en interne par les frottements s'il y en a.

En pratique, il importe de bien distinguer ces deux formes de chaleur, faute de quoi de graves erreurs de raisonnement peuvent être faites. En particulier, les transformations sans échange de chaleur avec l'extérieur, appelées adiabatiques, sont telles que 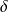Q = 0, qu'elles soient ou non le siège d'irréversibilités, c'est-à-dire que 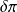soit nul ou non.