2 Etude d'une centrale électrique à vapeur
Le cycle de Hirn (ou de Rankine avec surchauffe) utilise un fluide condensable, qui est refroidi à une pression et une température suffisantes pour qu'il soit entièrement liquéfié avant compression. Dans ces conditions, le travail de compression devient quasiment négligeable devant le travail de détente (alors qu'il en représente environ 60 % dans une turbine à gaz). Le liquide comprimé est vaporisé et surchauffé dans la chaudière par échange thermique avec la source chaude, puis détendu et condensé. L'état diphasique du fluide lors des phases de condensation et de vaporisation est très favorable pour les échanges de chaleur.
Il est bien évidemment possible de modéliser directement ce cycle dans Thermoptim. Nous ne détaillerons pas ici complètement cette manière d'opérer, qui est bien documentée dans le guide de prise en mains relatif à la centrale à vapeur ou bien dans la séance Diapason S26 .
Nous en donnerons seulement un bref aperçu, après avoir présenté une manière de faire plus progressive qui peut bien convenir à des élèves débutants si l'enseignant souhaite qu'ils comprennent bien la manière dont les calculs sont effectués. Nous montrerons comment les élèves peuvent calculer le cycle pas à pas en procédant de deux manières différentes : tout d'abord en utilisant le calculateur-inverseur des propriétés des fluides, qui permet de ne pas faire appel à Thermoptim dans un premier temps, et ensuite en créant des points dans le progiciel. Une fois les points du cycle déterminés, ils peuvent être tracés dans les diagrammes thermodynamiques interactifs.
Cette manière de faire, qui diffère de la modélisation directe dans Thermoptim, présente sur le plan pédagogique l'intérêt que la démarche méthodologique de calcul d'un cycle doit être suivie de manière plus détaillée.
2.1 Présentation du cycle
le principe consiste à condenser l'eau à basse pression (et donc basse température), dans un échangeur en contact avec la source froide (généralement l'eau d'un fleuve ou l'air extérieur) : évolution (4-1). Au point 1, l'eau est à l'état liquide, à une température d'environ 20 °C, sous une faible pression (0,023 bar) ;
l'eau (à l'état liquide) est ensuite comprimée à une pression comprise entre 80 et 300 bars, selon les technologies utilisées : évolution (1-2). Pour une centrale électrique à flamme classique, la haute pression est voisine de 165 bars, ce qui représente un rapport de compression considérable (de l'ordre de 7 000). Cette compression peut en première approximation être supposée adiabatique, pour les raisons évoquées section 1.1.3, et même isentropique, les irréversibilités qui prennent place dans la pompe étant faibles ;
l'eau sous pression est ensuite chauffée à pression constante dans une chaudière à flamme (fuel, charbon, gaz naturel). L'échauffement comporte trois étapes :
chauffage du liquide dans l'économiseur, de près de 20 °C jusqu'à la température de début d'ébullition à la pression considérée (environ 355 °C pour 165 bars) : évolution (2-3a) ;
vaporisation à température constante dans le vaporiseur : évolution (3a-3b) ;
surchauffe jusqu'à la température maximale du cycle (560 °C) dans le surchauffeur : évolution (3b-3).
La vapeur est ensuite détendue dans une turbine de rendement isentropique voisin de 0,85, jusqu'à la pression de condensation évolution (3-4). L'évolution (3-4) est une détente adiabatique de 165 bars à 0,023 bar. Dans le cycle idéal, obtenu sans irréversibilités et donc à entropie constante, le point s'appelle 4s se trouve dans la zone mixte d'équilibre liquide-vapeur, son titre étant ici x = 0,74. Le point 4 correspondant au cycle réel est à la même pression que le point 4s mais son entropie est différente du fait des irréversibilités (plus grande d'après le second principe, ou bien en remarquant que ces irréversibilités ont pour effet d'augmenter l'enthalpie du fluide). Son enthalpie peut être déterminée si l'on connaît le rendement isentropique de la turbine.
Le mélange liquide-vapeur est enfin condensé jusqu'à l'état liquide dans un condenseur, échangeur entre le cycle et la source froide, par exemple ici l'eau d'un fleuve. Le cycle est ainsi refermé. Le schéma de la machine (figure ci-dessous) se déduit de ces considérations.
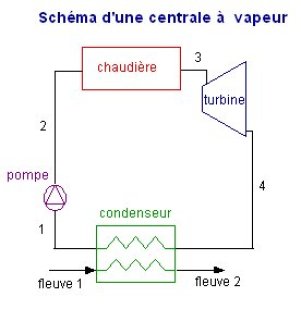
2.2 Technologie des composants
Une fois le schéma de principe de la machine ainsi défini, la discussion peut porter sur les technologies des divers composants. Les valeurs numériques qui ont été données dans la section précédente correspondent à un cycle de centrale thermique à flamme classique. Une telle centrale comprend quatre composants : une pompe, une chaudière, une turbine et un condenseur, traversés par le même débit d'eau. Pour les raisons exposées section 1.1.3, la pompe et la turbine peuvent être supposées adiabatiques. Quant à la chaudière et au condenseur, on peut en première approximation faire l'hypothèse qu'ils sont isobares (cf. sections 1.1.1 et 1.1.2).
La pompe est généralement du type centrifuge, multiétagée compte tenu du très haut rapport de compression à réaliser.
La chaudière remplit trois fonctions successives :
chauffer l'eau d'alimentation pressurisée jusqu'à la température de vaporisation à la pression correspondante ;
vaporiser l'eau ;
et enfin la surchauffer à la température désirée.
Elle se comporte donc comme un triple échangeur, et peut être représentée du point de vue des échanges thermiques par le schéma de la figure ci-dessous.

Les turbines à vapeur sont pour la plupart des turbines axiales multiétagées, qui peuvent être regroupées en deux grandes classes, selon la manière dont la détente se répartit entre le stator et le rotor :
les turbines à action, dans lesquelles toute la détente du fluide est alors réalisée dans les aubages fixes ou tuyères, en amont de la roue, et les pressions en amont et en aval du rotor sont égales ;
les turbines à réaction, dans lesquelles la détente est alors également répartie entre les tuyères du stator et la roue.
Chacun de ces deux types de turbine présente des avantages et des inconvénients qui lui sont propres : les turbines à action sont généralement utilisées pour les étages de tête des turbines multiétagées ou pour les unités de petite puissance, tandis que les turbines à réaction se révèlent bien adaptées pour les parties basse pression des turbines.
Le condenseur est un échangeur dont la particularité est de travailler en dépression par rapport à l'atmosphère, compte tenu de la faible tension de vapeur de l'eau à la température ambiante. La condensation à 20 °C implique que l'on maintienne dans le condenseur un vide assez poussé (0,023 bar), ce qui suppose un dispositif d'extraction de l'air complexe compte tenu des fuites inévitables, d'autant plus qu'il faut recourir à des turbines basse pression gigantesques compte tenu du très faible volume spécifique de la vapeur d'eau à 20 °C, qui impose de très grands débits-volumes, et donc des sections de passage et des vitesses très élevées. La fiche-guide de TD n°21 traite de ce sujet un peu difficile. Elle sera proposée dans les activités d'approfondissement présentées dans la quatrième partie.
2.3 Calcul du cycle pas à pas avec le calculateur-inverseur
Pour calculer ce cycle pas à pas, nous commencerons par utiliser le calculateur inverseur, sachant que le principal intérêt qu'il y a à procéder ainsi est d'une part de bien décomposer les différentes étapes et d'autre part de ne pas avoir dans un premier temps à introduire Thermoptim.
2.3.1 ETAT DU POINT 1
L'état du point 1 correspond au paramétrage du calculateur conformément à la figure du calculateur donnée ci-dessous. Le fluide sélectionné est l'eau, parmi les vapeurs condensables. Le calculateur doit être en mode de calcul (p,T,x) la pression étant égale à 0,023 bar, et la température de saturation imposée. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes (p et Pc sont en bar, h et u en kJ/kg, s en kJ/kg/K, v et Vc en m3/kg, M en kg et Tc en K) :
P | T (°C) | x | h | u | s | v | M | Pc | Tc | Vc |
0,023 | 19,746 | 0 | 82,837 | 82,834 | 0,29282 | 0,00100167 | 18,015 | 221,2 | 374,15 | 0,0032 |

2.3.2 ETAT DU POINT 2
Pour connaître l'état du point 2, le calculateur doit être paramétré en mode de calcul (p,s) la nouvelle pression étant égale à 165 bars, et l'entropie étant celle du point 1. Le calcul conduit à la figure ci-dessous.

La température du point a à peine augmenté, et le travail mis en jeu, égal à la variation d'enthalpie entre les points 1 et 2, vaut 99,297 – 82,837 = 16,46 kJ/kg.
On peut vérifier facilement qu'il est à peu près égal à
 , égal à 0,001 (16 500 – 2,3) = 16,5 kJ/kg, P étant exprimé en Pa.
, égal à 0,001 (16 500 – 2,3) = 16,5 kJ/kg, P étant exprimé en Pa.
Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :
P | T (°C) | x | h | u | s | v | M | Pc | Tc | Vc |
165 | 19,996 | 0 | 99,297 | 82,89 | 0,29282 | 0,00099438 | 18,015 | 221,2 | 374,15 | 0,0032 |
2.3.3 ETATS DES POINTS 3a ET 3b
Pour connaître l'état des points 3a et 3b, le calculateur doit être en mode de calcul (p,T,x) la pression restant égale à 165 bars, et la température de saturation étant imposée, x valant successivement 0 puis 1. Des copier-coller depuis le champ des résultats fournissent les valeurs suivantes pour les deux points :
P | T (°C) | x | h | u | s | v | M | Pc | Tc | Vc |
165 | 349,827 | 0 | 1670,52 | 1641,83 | 3,778 | 0,00173903 | 18,015 | 221,2 | 374,15 | 0,0032 |
et
P | T (°C) | x | h | u | s | v | M | Pc | Tc | Vc |
165 | 349,827 | 1 | 2568,79 | 2423,07 | 5,2202 | 0,00883163 | 18,015 | 221,2 | 374,15 | 0,0032 |
2.3.4 ETAT DU POINT 3
Pour connaître l'état du point 3, le calculateur doit être en mode de calcul (p,T,x) la pression restant égale à 165 bars, et la température valant 560 °C. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :
P | T (°C) | x | h | u | s | v | M | Pc | Tc | Vc |
165 | 560 | 1 | 3459,62 | 3113,52 | 6,4955 | 0,0209757 | 18,015 | 221,2 | 374,15 | 0,0032 |
La chaleur Q à fournir par la chaudière est égale à la variation d'enthalpie entre les points 2 et 3 : Q = 3360,32 kJ/kg.
2.3.5 ETAT DU POINT 4s
Pour connaître l'état du points 4s, le calculateur doit être paramétré en mode de calcul (p,s) la nouvelle pression étant celle de condensation, égale à 0,023 bar, et l'entropie étant celle du point 3. Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :
P | T (°C) | x | h | u | s | v | M | Pc | Tc | Vc |
0,023 | 19,746 | 0,74 | 1899,6 | 1799,68 | 6,4955 | 43,4468 | 18,015 | 221,2 | 374,15 | 0,0032 |
La variation d'enthalpie correspondant à la détente réversible est égale à h4s – h3, soit
 = -1560 kJ/kg. Sa valeur négative provient des conventions utilisées en thermodynamique, le travail étant fourni à l'extérieur du système considéré.
= -1560 kJ/kg. Sa valeur négative provient des conventions utilisées en thermodynamique, le travail étant fourni à l'extérieur du système considéré.
La valeur du travail de détente réel
 est, par définition du rendement isentropique
est, par définition du rendement isentropique
 , égal à
, égal à
 soit :
soit :
 = 0,85 (-1560) kJ/kg = -1326 kJ/kg
= 0,85 (-1560) kJ/kg = -1326 kJ/kg
L'enthalpie du point 4 est donc égale à celle du point 3 plus
 (en valeur algébrique), soit 2133,61 kJ/kg
(en valeur algébrique), soit 2133,61 kJ/kg
2.3.6 ETAT DU POINT 4
Pour connaître l'état du points 4, le calculateur doit être paramétré en mode de calcul (p,h) la pression restant égale à 0,023 bar, et l'enthalpie étant celle du point 4. Le calcul conduit à la figure ci-dessous.

Le titre en sortie de turbine vaut 0,835.
Un copier-coller depuis le champ des résultats fournit les valeurs suivantes :
P | T (°C) | x | h | u | s | v | M | Pc | Tc | Vc |
0,023 | 19,746 | 0,835 | 2133,61 | 2020,81 | 7,2944 | 49,04266 | 18,015 | 221,2 | 374,15 | 0,0032 |
2.3.7 BILAN GLOBAL DU CYCLE
Les calculs précédents ont permis d'estimer la chaleur Q fournie par la chaudière (3360,32 kJ/kg), et le travail net est égal en valeur absolue à la différence entre celui produit par la turbine (1326 kJ/kg) et celui consommé par la pompe (16,4 kJ/kg), soit 1309,55 kJ/kg.
Le rendement du cycle est égal au rapport de ces deux valeurs. Il vaut donc
 = 1309,55/3360,32 = 38,97 %.
= 1309,55/3360,32 = 38,97 %.
2.4 Calcul du cycle pas à pas avec les points de Thermoptim
Les écrans des points de Thermoptim permettent de faire les mêmes calculs que ceux que nous venons d'effectuer. Comme nous allons le voir, les résultats sont identiques, mais cela suppose de tout de suite initier les élèves à une partie des fonctionnalités du simulateur.
Tant que l'on ne définit pas les transfos, l'éditeur de schémas ne doit pas être utilisé. Les points peuvent en effet être directement créés depuis l'écran du simulateur, en double-cliquant sur le bandeau de la table des points. Une fois qu'un point existe, le bouton « Dupliquer » permet d'en générer un autre sans avoir à entrer le corps.
2.4.1 ETAT DU POINT 1
L'état du point 1 est donné figure ci-dessous. La pression est entrée, l'option "imposer la température de saturation" sélectionnée, avec un titre égal à 0.

2.4.2 ETAT DU POINT 2
Pour connaître l'état du point 2, le point doit être paramétré en mode de calcul « P et s connus », la nouvelle pression étant égale à 165 bars, et l'entropie étant celle du point 1. Le calcul conduit à la figure ci-dessous.

La température du point 2 a à peine augmenté, et le travail mis en jeu, égal à la variation d'enthalpie entre les points 1 et 2, vaut 99,297 – 82,837 = 16,46 kJ/kg.
On peut vérifier facilement qu'il est à peu près égal à
 , égal à 0,001 (16 500 – 0,23) = 16,5 kJ/kg, P étant exprimé en Pa.
, égal à 0,001 (16 500 – 0,23) = 16,5 kJ/kg, P étant exprimé en Pa.
2.4.3 ETATS DES POINTS 3a ET 3b
Pour connaître l'état des points 3a et 3b, le paramétrage doit être "P et T connus", la pression restant égale à 165 bars, et la température de saturation étant imposée, x valant successivement 0 puis 1.
2.4.4 ETAT DU POINT 3
Pour connaître l'état du point 3, le paramétrage doit être « P et T connus », la pression restant égale à 165 bars, et la température valant 560 °C.
La chaleur Q à fournir par la chaudière est égale à la variation d'enthalpie entre les points 2 et 3 : Q = 3360,32 kJ/kg.
2.4.5 ETAT DU POINT 4s
Pour connaître l'état du point 4s, le paramétrage doit être « P et s connus », la nouvelle pression étant celle de condensation, égale à 0,023 bar, et l'entropie étant celle du point 3.
La variation d'enthalpie correspondant à la détente réversible est égale à h4s – h3, soit
 = -1560 kJ/kg. Sa valeur négative provient des conventions utilisées en thermodynamique, le travail étant fourni à l'extérieur du système considéré.
= -1560 kJ/kg. Sa valeur négative provient des conventions utilisées en thermodynamique, le travail étant fourni à l'extérieur du système considéré.
La valeur du travail de détente réel
 est, par définition du rendement isentropique
est, par définition du rendement isentropique
 , égal à
, égal à
 soit :
soit :
 = 0,85 (-1560) kJ/kg = -1326 kJ/kg
= 0,85 (-1560) kJ/kg = -1326 kJ/kg
L'enthalpie du point 4 est donc égale à celle du point 3 plus
 (en valeur algébrique), soit 2133,61 kJ/kg
(en valeur algébrique), soit 2133,61 kJ/kg
2.4.6 ETAT DU POINT 4
Pour connaître l'état du point 4, le paramétrage doit être "P et s connus", la pression restant égale à 0,023 bar, et l'enthalpie étant celle du point 4. Le calcul conduit à la figure ci-dessous. Le titre en sortie de turbine vaut 0,835.

2.4.7 BILAN GLOBAL DU CYCLE
Les calculs précédents ont permis d'estimer la chaleur Q fournie par la chaudière (3360,32 kJ/kg), et le travail net est égal en valeur absolue à la différence entre celui produit par la turbine (1326 kJ/kg) et celui consommé par la pompe (16,4 kJ/kg), soit 1309,55 kJ/kg.
Le rendement du cycle est égal au rapport de ces deux valeurs. Il vaut donc
 = 1309,55/3360,32 = 38,97 %.
= 1309,55/3360,32 = 38,97 %.
2.5 Modélisation directe dans Thermoptim
La modélisation directe du cycle dans Thermoptim est celle qui est présentée de manière détaillée dans le guide de prise en mains relatif à la centrale à vapeur et dans la séance Diapason S26. Nous nous contenterons ici d'en rappeler les grandes lignes.
2.5.1 CREATION DU SCHEMA
Dans cette approche, l'élève commence par travailler avec l'éditeur de schémas, plaçant les différents composants sur la palette et saisissant pour chacun d'eux un tout petit nombre d'informations. Il aboutit ainsi à un schéma du type de celui présenté figure ci-dessous, qu'il transfère dans le simulateur : la seule différence avec le schéma-bloc est l'apparition des trois parties de la chaudière, préalablement non distinguées.

2.5.2 PARAMETRAGE DU CYCLE
Dans un second temps, l'élève paramètre sur le plan thermodynamique les points dont l'état est parfaitement connu (1, 3a, 3b, 3), et les transfos compression et détente, ce qui permet de calculer les deux autres points.
2.5.3 COMPARAISON DES DEUX APPROCHES PEDAGOGIQUES
L'intérêt de la modélisation directe dans Thermoptim est qu'elle se fait dans un premier temps dans l'éditeur de schémas, l'architecture du cycle étant très proche de celle du schéma-bloc.
L'élève commence donc par réfléchir à la structure globale du cycle, sans avoir à se préoccuper de la manière dont les calculs sont effectués dans chaque composant. La modélisation est grandement facilitée, ce qui est un atout sur le plan psychologique, car l'élève est vraiment convaincu que le simulateur lui permet de "faire de la thermo sans peine". Il est donc encouragé à continuer, ses appréhensions initiales vis à vis de la discipline s'estompant.
Le risque est qu'il ait tendance à utiliser le logiciel de façon "presse-bouton", sans bien comprendre la méthodologie sous-jacente. Le parti pris pédagogique est donc un peu différent de celui qui a été retenu dans les sections 2.3 et 2.4, où l'enseignant considère fondamental que l'élève ait pleinement conscience de l'enchaînement des calculs.
Dans tous les cas, les calculs sont effectués par un logiciel, ce qui correspond bien au même paradigme global, celui de la réduction des difficultés calculatoires, mais le degré d'implication de l'élève n'est pas le même. Les deux approches pédagogiques constituent donc des variantes entre lesquelles l'enseignant choisira, en fonction du contexte auquel il est confronté.
2.6 Représentation dans les diagrammes
Une fois les points du cycle déterminés, il est possible de le tracer dans les diagrammes usuels, notamment les diagrammes entropique, des frigoristes et de Mollier.
Dans ce qui précède, nous avions introduit les points 4s et 4, le premier étant un intermédiaire qui n'a pas besoin d'être représenté. Dans ce qui suit, pour simplifier les notations, nous n'afficherons que le point 4.
Si le cycle a été calculé en créant des points dans Thermoptim, comme expliqué dans les sections 2.3 ou 2.5, leur tracé dans les diagrammes peut être directement effectué en utilisant l'interface entre le simulateur et les diagrammes. S'il a été calculé avec le calculateur-inverseur, il faut commencer par créer les points dans le simulateur.
2.6.1 SAISIE DIRECTE DES POINTS DANS L'EDITEUR DE CYCLES
Il est possible d'enter directement les points dans l'éditeur de cycles du diagramme, en opérant de la manière suivante.
Une fois le diagramme des vapeurs de l'eau ouvert, l'éditeur de cycles est accessible à partir du menu Cycle ou en tapant Ctrl C (figure ci-dessous).
En utilisant le bouton Insérer, il est alors possible d'entrer les différents points un par un. La seule contrainte est que, le bouton de recalcul n'étant pas disponible dans la version Education Salle de cours de Thermoptim, il faut entrer à la main toutes les valeurs des variables (T, P, x, s et h) pour que le cycle soit correctement construit.
Notons qu'une fois ces points créés dans l'environnement des diagrammes, il est possible de les transférer dans le simulateur en utilisant l'interface qui les relie.
Dans l'écran de l'interface (figure ci-dessous), il faut commencer par mettre à jour la table des points, puis mettre à jour le simulateur à partir du diagramme.

Les points sont alors créés dans le simulateur. Une fois ce transfert effectué, il est toutefois préférable de reprendre les paramétrages des points un par un, notamment pour imposer la température de saturation lorsque nécessaire.
2.6.2 TRACE DANS LE DIAGRAMME ENTROPIQUE
Sur le diagramme entropique (figure ci-dessous), pour augmenter la lisibilité, on n'a fait apparaître que les isobares (en bleu), et les isenthalpes (en rouge). Les points 1 et 2 représentant la compression à l'état liquide sont quasiment superposés, et l'échauffement à l'état liquide presque confondu avec la courbe de saturation liquide. La vaporisation se fait selon un segment de droite horizontal.
Les trois étapes de l'échauffement sont bien visibles :
chauffage du liquide dans l'économiseur, de près de 20 °C jusqu'à la température de début d'ébullition à la pression considérée (environ 355 °C pour 165 bars) : évolution (2-3a) ;
vaporisation à température constante dans le vaporiseur : évolution (3a-3b). La vaporisation s'effectuant à pression et température constantes, elle se traduit sur le diagramme entropique par un segment horizontal 3a-3b. Le point 3b se trouve donc sur la branche descendante de la courbe de vaporisation, ou courbe de rosée, à son intersection avec la droite horizontale de température 355 °C, toujours à la pression P2 de 165 bars ;
surchauffe jusqu'à la température maximale du cycle (560 °C) dans le surchauffeur : évolution (3b-3). Le point 3 se trouve donc à l'intersection de l'isobare P = 165 bars et de l'horizontale d'ordonnée T = 560 °C.

La surchauffe isobare correspond à la pointe maximale du cycle, et la détente irréversible se traduit par une augmentation de l'entropie, le point 4 étant situé dans la zone d'équilibre liquide-vapeur (titre égal à 0,835).
La forme de ce cycle s'écarte assez sensiblement de celle de celui de Carnot, compte tenu de l'allure des isobares. Il est possible de l'améliorer en procédant à des resurchauffes qui conduisent à une détente dite para-isotherme, et à des prélèvements qui permettent d'effectuer une régénération partielle. De telles variantes seront proposées aux élèves dans l'étape de consolidation de leurs connaissances (cf. troisième partie).
2.6.3 TRACE DANS LE DIAGRAMME DES FRIGORISTES
Sur le diagramme des frigoristes (h, log P) (figure ci-dessous), pour augmenter la lisibilité, on n'a fait apparaître que les isothermes (en bleu), et les isentropes (en rouge). La compression à l'état liquide est ici représentée par le segment (1 - 2) quasiment vertical très visible.

Si l'on néglige les pertes de charge dans le générateur de vapeur ou la chaudière, l'ensemble de l'échauffement correspond à l'horizontale (2-3), les trois parties représentant l'économiseur, le vaporiseur et le surchauffeur apparaissant très distinctement. La détente irréversible se traduit par une augmentation de l'entropie, le point 4 étant situé dans la zone d'équilibre liquide-vapeur.
Comme on le voit sur cet exemple, la représentation du cycle dans le diagramme (h, log P) est très parlante sur le plan physique : les échanges de chaleur, quasiment isobares, correspondent aux segments horizontaux, et les compressions et les détentes sont proches des isentropes, d'autant moins pentues que l'on s'écarte de la zone liquide.
2.6.4 TRACE DANS LE DIAGRAMME DE MOLLIER
Sur le diagramme de Mollier (figure ci-dessous), dont on n'a fait, pour des raisons de lisibilité, apparaître que la partie droite et seulement les isobares (en bleu) et les isothermes (en rouge), les points 1 et 2 (hors figure) représentant la compression à l'état liquide sont quasiment superposés, et l'échauffement à l'état liquide presque confondu avec la courbe de saturation liquide. La vaporisation se fait selon un segment de droite de pente T.

La surchauffe isobare correspond à la pointe maximale du cycle, et la détente irréversible se traduit par une augmentation de l'entropie, le point 4 étant situé dans la zone d'équilibre liquide-vapeur (titre égal à 0,835).
2.7 Création dans Thermoptim des transfos à partir des points
Si le cycle a été modélisé sans utiliser l'éditeur de schémas de Thermoptim, (cf. sections 2.3 et 2.4), et que les points du cycle ont été créés ou transférés dans le simulateur afin de pouvoir les représenter dans les diagrammes, le projet se présente comme indiqué figure ci-dessous.

Pour finir de représenter le cycle dans Thermoptim, il faut maintenant relier ces points par des transfos, ce qui peut être fait très simplement à partir de l'éditeur de schémas. Il suffit pour cela de sélectionner dans la palette les différents composants, en entrant dans les champs définissant les ports d'entrée et de sortie leurs différents noms et leur corps (de l'eau).
Les points étant tous connus, les transfos doivent être initialement paramétrées en conséquence. En particulier la pompe et la turbine doivent recalculer la valeur du rendement, le point aval étant connu.
Une fois ces valeurs déterminées, le paramétrage peut être changé si l'on désire pouvoir simuler d'autres cas.
Le synoptique de l'installation se déduit des remarques précédentes (figure ci-dessous). Il correspond bien sûr au schéma de la figure de la section 2.5.1, auquel on a ajouté les sources de chaleur externes pour montrer que la machine interagit avec son environnement. On a aussi fait apparaître le cartouche avec le bilan du cycle, et on retrouve bien les valeurs qui avaient été déterminés par le calcul pas à pas.

Ce cycle peut être directement obtenu en chargeant dans Thermoptim l'exemple intitulé « t1_6.1 cycle à vapeur simple » à partir du catalogue d'exemples.
2.8 Activités pédagogiques connexes avec les élèves
2.8.1 Diagrammes thermodynamiques
L'utilisation des seuls diagrammes thermodynamiques permet déjà de faire effectuer aux élèves de nombreuses activités intéressantes relatives aux fluides, préalables à l'étude des composants et des systèmes :
en premier lieu, bien évidemment, discuter de l'intérêt des différents types de diagrammes et de leur construction. Les explications données dans le portail permettent de le faire dans une très large mesure ;
l'enseignant peut demander aux élèves de construire pas à pas les diagrammes, en affichant successivement les différentes courbes d'isovaleurs, et en cherchant à chaque fois une explication à la forme qu'elles prennent : pourquoi y a-t-il ou non changement de pente au niveau de la courbe de saturation...
il est aussi intéressant de visualiser la zone des gaz parfaits, qui est très limitée sur les diagrammes des vapeurs : il s'agit de leur partie inférieure droite, où par exemple, dans le diagramme entropique, les isenthalpes se rapprochent de l'horizontale, et dans le diagramme des frigoristes, les isothermes de la verticale. Il est alors clair que les transformations ne peuvent pas être calculées avec précision si l'on fait l'hypothèse des gaz parfaits ;
dans la zone d'équilibre liquide-vapeur, on peut remarquer que les isobares et les isothermes sont des segments horizontaux confondus, étant donné que la pression et la température sont liées par la loi de pression saturante ;
tracer les évolutions typiques dans les diagrammes (on crée pour cela deux points dans le simulateur, que l'on calcule, puis transfère dans les diagrammes) ;
illustrer, dans le diagramme des gaz idéaux, la relation Cp > Cv en étudiant les pentes des isobares et des isochores ;
les diagrammes permettent aussi aux élèves de réfléchir au nombre de variables indépendantes nécessaires pour calculer l'état d'un fluide, aux notions de grandeurs intensives[1] et extensives[2]...
2.8.2 Cycle de centrale à vapeur
Autour du cycle de centrale à vapeur, de nombreuses activités intéressant les élèves peuvent prendre place :
en premier lieu, bien évidemment, discuter de l'intérêt des différents types de diagrammes (l'enseignant qui le désire pourra pour cela se référer à la section 2.6.6.1 de [1]).
réfléchir sur la notion d'efficacité du cycle, égale au rapport de l'énergie utile (ici essentiellement le travail de détente) à l'énergie payante (ici la chaleur fournie par la chaudière) ;
comparer cette valeur avec celle du cycle de Carnot fonctionnant entre 20 °C (source froide) et 560 °C (température maximale du cycle), pour se faire une idée de l'écart du cycle réel (0,39) par rapport au cycle idéal (0,65). D'une manière plus générale, discuter des écarts entre le cycle réel et celui de Carnot ;
étudier l'évolution de l'efficacité du cycle et de la puissance produite lorsque la pression et la température du cycle varient ;
comparer qualitativement ce cycle par rapport au cycle de Carnot, en identifiant les écarts qui existent entre eux.
Des études de variantes peuvent ensuite être proposées. On pourra en particulier se référer au chapitre 6 de la référence [2], où sont proposés divers exemples, qui seront aussi repris dans les activités de la deuxième étape de formation des élèves :
une première idée pour améliorer le cycle de Hirn consiste à se rapprocher du cycle de Carnot en effectuant des resurchauffes (ou réchauffes). Dans ce cas, on commence par détendre partiellement le fluide, puis on le refait passer dans la chaudière, où il est réchauffé, à la nouvelle pression, jusqu'à la température maximale du cycle. Cette opération peut le cas échéant être répétée plusieurs fois, générant ce que l'on appelle une para-isotherme ;
une autre manière d'améliorer le cycle consiste à effectuer une régénération au moins partielle, en utilisant une partie de l'enthalpie disponible en fin de détente pour préchauffer l'eau comprimée à l'état liquide ;
le cycle à prélèvement et réchauffe (avec par exemple un taux de prélèvement égal à 15 %, et une température de réchauffe identique à celle de surchauffe initiale) correspond à la combinaison de ces deux améliorations ;
un cycle à vapeur supercritique avancé à deux réchauffes, étudié comme cas limite compte tenu des niveaux de pression et de température choisis : pressions égales à 0,023, 6,5, 76 et 415 bars, et température de surchauffe et de réchauffe de 704 °C ;
un cycle de centrale nucléaire du type Réacteur à Eau Pressurisée (REP), dont la pression dans le générateur est voisine de 60 bars, et la température de la vapeur 275 °C.
2.9 Exploration de cycles existants
Dans ce qui précède, nous avons montré comment calculer pas à pas le cycle de la centrale à vapeur, puis comment le modéliser dans Thermoptim, en partant du principe que l'objectif pédagogique visé était d'apprendre aux élèves à acquérir ce savoir-faire tout en assimilant des connaissances déclaratives suffisantes pour comprendre les fondements de ces opérations.
Il existe cependant des contextes pédagogiques où cette manière de procéder ne peut pas être adoptée, essentiellement par manque de temps, et où cependant l'enseignant souhaite que ses élèves puissent utiliser Thermoptim et les diagrammes interactifs, sans construire par eux-mêmes les modèles.
C'est par exemple le cas dans certaines Classes Préparatoires aux Grandes Ecoles (CPGE) où le volume horaire est insuffisant pour opérer comme nous l'avons fait dans les sections précédentes. Pourtant, de nombreux enseignants considèrent pédagogiquement pertinent d'utiliser Thermoptim, car cela permet aux élèves de voir comment les équations qu'ils étudient peuvent être mises en application. Leur programme acquiert ainsi dans leur esprit davantage de sens : il correspond à un savoir qui peut être vraiment utilisé.
Dans de tels cas, une alternative pédagogique à celles que nous avons présentées jusqu'ici consiste à faire travailler les élèves sur des exemples déjà modélisés, en leur demandant de les explorer et de les comprendre. Ils peuvent aussi modifier les paramétrages et réaliser quelques études de sensibilité.
S'il souhaite faire étudier la centrale à vapeur simple de cette manière, l'enseignant sélectionne alors dans le catalogue d'exemples de Thermoptim l'exemple intitulé "t1_6.1 cycle à vapeur simple" à partir du catalogue d'exemples et demande à ses élèves de le charger.
Le projet étant chargé, il commence par passer en revue les différents composants, en fournissant à ses élèves des explications technologiques et thermodynamiques. Ensuite, il peut leur demander de procéder à des changements de paramétrage et d'en étudier l'impact sur les performances globales du cycle.
Même si elle peut paraître un peu limitée, cette approche pédagogique peut se révéler très féconde, les élèves s'impliquant souvent beaucoup plus lorsqu'ils ont un simulateur à leur disposition que devant une feuille de papier ou un tableau. Elle est en particulier souvent appropriée en formation professionnelle, les élèves étant généralement assez réticents devant les approches disciplinaires académiques. Ils préfèrent avoir l'outil logiciel entre leurs mains pour pouvoir l'explorer à leur guise et poser des questions aux enseignants qui les encadrent.

