Representation of real fluids
The increase in pressure and/or lowering of the temperature can justify a reconsideration of the ideal gas equation PV = RT. This is especially the case near the liquid-vapor equilibrium zone.
When the fluid no longer satisfies the ideal gas equation, its internal energy and enthalpy are no longer based solely on temperature.
This behavior is shown in Figure below, for superheated steam. It is clear that the heat capacity cp of this substance is the more affected by the pressure as it is higher and the temperature is lower (that is to say, especially in the immediate vicinity of the saturation curve).
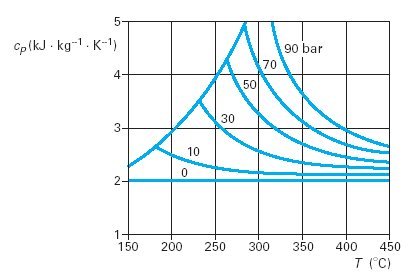
To determine the state of a real fluid, usually a thermodynamic diagram, a table of values of the thermodynamic properties, or a set of equations of state covering the various necessary regions is used.
Thermodynamic diagrams
Traditionally, thermodynamic diagrams are mostly used. However, there is a marked evolution of the practice, development of computer making possible the direct calculation of thermodynamic properties of fluids in a wide range of variation of state variables. Thermoptim allows you to perform such calculations.
Even if one has a calculator of fluid properties, such as the Thermoptim-Light calculator available on this portal, diagrams retain great interest at educational level, because they can easily display the properties of real gases, including the liquid-vapor equilibrium area.
For more information on pure substance diagrams, we recommend that you view the following Diapason session:
Equations of state (EOS)
Available fluid models vary depending on the use, the accuracy, acceptable computation time, the properties that you need to calculate, as well as your own modeling capabilities.
Several state equation families exist, the oldest being the cubic EoS, which are presented in the page on the calculation of thermodynamic and phase equilibria properties of pure substances and mixtures.
However, the cubic EOS do not adequately represent the fluids whose molecules are not spherical or that have hydrogen bonds. New equations of state have recently been proposed for these types of fluids, such as equation Cubic Plus Association (CPA), which adds additional terms to the equation of a cubic EOS, and the family of equations derived from Statistical Associating Fluid Theory (SAFT). A portal page is dedicated to them.
It is finally not always possible to adequately represent the properties of a fluid using a single equation, as is the case for water. The reference software packages for calculating its properties involve numerous parameters and different equations depending on the region.
Cutting diagram in regions: the case of water
For example, the International Committee of Formulation of the Sixth Conference on Properties of Steam in 1967 chose a division into six work regions:
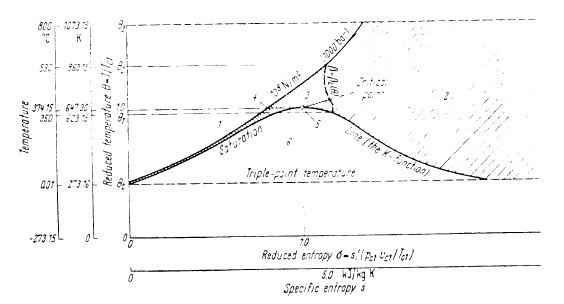
Conventionally , one must differentiate between the liquid zone (1), the steam zone (2) , the saturation curve (5), and the liquid-vapor equilibrium zone (6). For these zones, the calculation is based on the temperature T, the pressure P or the saturation pressure Psat.
When the temperature exceeds the 350 °C (623.15 K), two new zones appear, one (4) for the liquid, the other ( 3) for steam, where the calculation is done from the temperature T and the volume v.
Separation of liquid zones 1 and 4 is simple: it depends only on the temperature, as for zones 4 and 3, defined by the critical isotherm.
The separation of zones 2 and 3 is more complex: it depends on the pressure by a function beta_l(T).
In practice, if P < beta_l (T), the point is located in Zone 2, and otherwise in Zone 3, this as long as T < 590 °C (863.15 K). For higher temperatures, it is in zone 2.
When the point is located in zones 3 and 4, and only T and P are known, we must reverse the function P (v, T), to find the value of the corresponding volume. Theoretically this is not a problem, but in practice the difficulty is that the upper and lower range resolution limits change depending on whether the point is in subcritical or supercritical for zone 3, and differ from those of zone 4. Their choice depends on the temperatures and must be done carefully, otherwise the algorithm finds a solution, but it is not the right one...
The equations of water still the most widely used today date from 1967. They are the ones that are included in the tables of the ASME or Thermoptim. In 1997, new, more accurate and easier to solve numerically formulations have been adopted, but their use is not yet widespread in the industry.
