Représentation des propriétés des corps purs
Phases solide, liquide, gazeuse
Un corps pur peut se présenter sous l'une ou plusieurs des trois phases solide, liquide ou gazeuse, l'état solide pouvant même comporter plusieurs variétés dites allotropiques, qui traduisent les différents arrangements possibles du réseau cristallin.
Ces trois phases se distinguent, au plan microscopique, par l'intensité des forces intermoléculaires. A l'état solide, ces dernières ne permettent aux atomes que d'osciller autour de positions fixes de distribution aléatoire ou ordonnée (cristaux).
Leur intensité diminue dans les liquides, qui n'ont pas de forme propre, mais restent faiblement compressibles. On parle alors d'ordre à faible distance et de désordre à longue distance. Dans un gaz, les forces intermoléculaires sont très faibles, et les molécules animées de mouvements désordonnés.
Lorsqu'on chauffe un solide à pression constante bien choisie, il se transforme en liquide, et on parle de fusion. Si l'on continue à apporter de la chaleur, le liquide se transforme en vapeur, et on parle de vaporisation. Il est aussi possible qu'un solide se transforme directement en vapeur, ce qui s'appelle une sublimation. La température[1] à laquelle ces transformations se réalisent dépend de la pression exercée sur le corps considéré. Par exemple à la pression atmosphérique, le CO2 se sublime, c'est-à-dire passe directement de l'état solide à l'état gazeux, tandis que l'eau bout à 100 °C.
Lorsqu'une masse donnée d'un corps pur se présente sous une seule phase[2], son état est défini par deux variables, par exemple sa pression et sa température[1]. Dans le plan (P,T) (figure ci-dessous), les trois phases correspondent à trois domaines, séparés par trois courbes de saturation (sublimation, vaporisation et fusion) se rejoignant au point triple T.
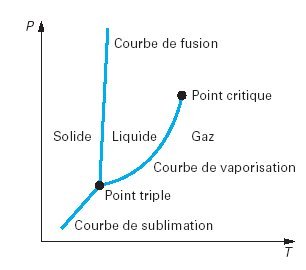
Chacune des courbes correspond à un équilibre diphasique. Par exemple, la courbe la plus à droite est l'ensemble des points figuratifs de l'équilibre d'un liquide avec sa vapeur. L'équilibre diphasique suppose donc que la pression et la température vérifient une relation caractéristique de la nature du fluide.
Pour que chacun de ces changements de phase puisse se réaliser, il est nécessaire de fournir ou de retirer de l'énergie, appelée chaleur latente de changement d'état. Au cours du changement d'état, on observe des va-riations importantes du volume spécifique, sauf pour la fusion-solidification. C'est notamment le cas lors de la vaporisation, la vapeur étant de l'ordre de 600 à 1000 fois moins dense que le liquide. Cette modification de volume spécifique se fait à pression et température constantes.
Donnons quelques exemples illustrant soit l'utilisation pratique des changements de phase, soit les contraintes induites par la présence d'un équilibre liquide-vapeur :
Lorsqu'on ajoute des glaçons à une boisson tiède, elle leur fournit de la chaleur qui les fait fondre, ce qui la rafraîchit. Comme la chaleur latente de fusion de la glace est bien supérieure à la capacité thermique massique de la boisson, on obtient l'effet de refroidissement recherché sans apporter trop d'eau de dilution.
Pour transporter le méthane sur de longues distances par voie maritime, on le liquéfie à une température de - 160 °C environ, réduisant 600 fois son volume massique par rapport au gaz. Il est ainsi possible de le maintenir à la pression atmosphérique dans les cuves du méthanier. Bien que ces cuves soient très bien isolées, on ne peut éviter quelques échanges de chaleur avec le milieu environnant, qui ont pour effet de vaporiser une petite quantité de gaz, laquelle est utilisée pour la propulsion du navire.
A contrario, le gaz butane ou propane distribué pour les usages culinaires est confiné à l'état liquide à température ambiante dans des bouteilles métalliques épaisses, ceci afin de résister à la pression de quelques dizaines de bars qui s'établit à l'intérieur.
Toutes les cuissons réalisées à l'eau bouillante prennent place à 100 °C si la pression est égale à 1 atmosphère, et ceci quelle que soit la puissance thermique fournie à la cuisson. C'est ainsi que l'on peut définir avec précision le temps de cuisson pour une recette culinaire, par exemple d'un oeuf à la coque.
Le principe de la cocotte minute est de s'affranchir de cette limite de 100 °C en effectuant la cuisson dans une enceinte à une pression supérieure à 1 atm. On peut atteindre ainsi 110 °C ou 120 °C, ce qui permet de cuire plus rapidement les aliments.
Un exemple de condensation est celle qui se dépose sur des surfaces froides au contact avec de l'air humide, comme la buée sur une vitre, ou la rosée du matin sur des feuilles.
Le point triple correspond à l'état où il est possible de maintenir en équilibre les trois phases simultanément. Le point critique représente l'état où la phase de pure vapeur a les mêmes propriétés que la phase de liquide pur. A des températures et pressions plus élevées (supercritiques), il n'est pas possible d'observer une séparation entre les phases liquide et gazeuse : le ménisque de surface qui sépare les phases liquide et vapeur disparaît au point critique.
En pratique, dans les machines thermiques, les fluides se présentent le plus souvent à l'état gazeux ou liquide, ou bien sous forme d'un mélange de phase gazeuse et de phase liquide. Pour en calculer les propriétés, on est amené à distinguer deux grandes catégories de fluides : les gaz idéaux, qui peuvent être purs ou composés, et qui incluent les gaz parfaits, et les fluides réels condensables, qui peuvent eux aussi être purs ou composés.
Dans le noyau de Thermoptim, tous ces types de fluide sont représentés, à l'exception des mélanges de fluides réels, mais ceux-ci peuvent être modélisés par des mélanges externes, en utilisant les bibliothèques TEP Lib et CTP Lib.
Dans ce portail, des pages spécifiques traitent :
Dans ce qui suit, nous parlerons des liquides et des solides ainsi que des propriétés des mélanges de phases en équilibre liquide-vapeur.
Liquides et solides
Les liquides et les solides sont qualifiés d'idéaux lorsque leur compressibilité est négligeable (v = Cste).
Puisqu'un liquide ou un solide "idéal" ne peut être soumis à aucun mode de travail réversible, une seule variable bien choisie suffit à en représenter l'état thermodynamique.
On peut en effet considérer que l'énergie interne d'un liquide ou d'un solide idéal ne dépend que de sa température :
du/dT = c, comme pour un gaz parfait.
En revanche l'enthalpie du liquide idéal (celle du solide n'a pas de sens physique) fait encore intervenir la pression :
dh = cdT + vdP
On peut encore définir l'entropie : ds = 1/T du + P/T dv, ce qui donne :
ds = c dT/T
Comme pour les gaz, on qualifie de "parfait" un liquide ou un solide dont la capacité thermique massique ne varie pas significativement : c = Cste.
On obtient alors :
u - u0 = c (T - T0)
h - h0 = c ( T - T0) + v ( P - P0)
s - s0 = c ln(T/T0)
En pratique, c'est souvent à la pression de saturation que sont repérées les caractéristiques des liquides. Toutefois, la correction v ( P - P0) étant généralement faible, cette convention a peu d'importance.
Pour une évolution isobare, le calcul des propriétés thermodynamiques des liquides ne fait intervenir que leur capacité thermique massique.
Équilibre liquide - vapeur d'un corps pur
Dans les machines à fluide compressible, il est fréquemment nécessaire d'étudier des transformations amenant le fluide à l'état liquide. Le gaz parfait jusqu'au zéro absolu n'existant pas, tous les fluides sont condensables, et il est nécessaire de connaître leurs propriétés jusqu'à l'état liquide.
L'étude de l'équilibre liquide-vapeur est basée sur la loi du mélange des phases qui ne fait que traduire l'extensivité des fonctions d'état avec l'hypothèse que l'énergie interfaciale est négligeable, et qui s'énonce : le volume, l'énergie interne, l'enthalpie, l'entropie d'un mélange de phases, à la pression P et à la température T, sont respectivement les sommes de ces grandeurs relatives aux différentes phases formant le mélange, prises isolément à la même pression et à la même température.
Sur les différents diagrammes thermodynamiques des corps purs, la zone de vaporisation ou d'équilibre liquide-vapeur apparaît clairement pour des températures et pressions inférieures à celles du point critique. Cette zone est limitée à gauche par la courbe de liquide saturé, et à droite par la courbe de vapeur saturée sèche. Ces deux courbes constituent la courbe de saturation, à la forme caractéristique. Entre ces deux courbes, la pression et la température ne sont plus indépendantes : elles sont reliées par une relation, que l'on appelle loi de pression saturante ou de tension de vapeur, et le système est monovariant.
Loi de pression saturante
Pour représenter algébriquement la loi de pression saturante, de nombreuses formules ont été proposées. L'une des plus employées est celle d'Antoine :
ln(Ps) = A - B/(C+T)
où A, B et C sont des paramètres caractéristiques du fluide, et Ps la pression de vapeur saturante.
Avec Ps en bars et T en K, on a par exemple pour l'eau : A = 11,783 B = 3895,65 C = - 42,1387
Cette formule n'est cependant pas très précise, et, dans Thermoptim, le développement suivant a été retenu :
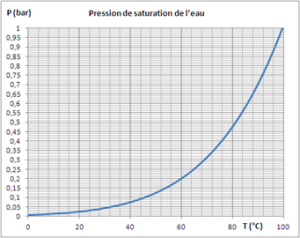
A titre d'exemple, cette figure présente la loi de pression saturante de l'eau Pvs(T), en dessous de 100 °C, température de saturation de l'eau à 1 atm, c'est-à-dire environ 1 bar. Elle montre que la pression de saturation de l'eau à température ambiante est très basse. Pour 20 °C, elle est de l'ordre de 0,025 bar. |
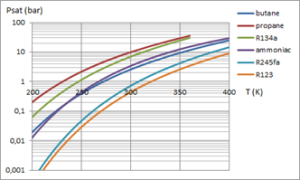
Pour une application donnée, la loi de pression saturante est l'un des critères de sélection d'un fluide de travail. Ces courbes donnent les lois de pression saturante de divers fluides. |
Titre en vapeur
Dans la partie médiane de la zone d'équilibre liquide-vapeur, le fluide se présente à la fois sous les deux phases, liquide et vapeur. Dans cette zone centrale, les isobares et les isothermes sont confondues, le changement d'état liquide - vapeur se faisant à température et pression constantes. La composition du mélange est définie par son titre x, rapport de la masse de vapeur mg à la masse totale (mg plus la masse de liquide ml).
x = mg/(mg + ml) (16)
Enthalpie de vaporisation
La longueur du palier de vaporisation, à un facteur près dans les représentations entropique (s,T) et de Mollier (s,h), et directement dans le diagramme des frigoristes, donne l'enthalpie de vaporisation L du fluide aux conditions P et T considérées :
hg - hl = L
sg - sl = L/T
Les relations ci-dessus peuvent être démontrées à partir de la relation exprimant que l'enthalpie libre est minimale à l'équilibre : au cours du processus de vaporisation, l'enthalpie libre évolue de gl à gg.
Si l'évolution est réversible, on a : dg = 0, ou encore gl = gg :
hl - T sl = hg - T sg
On retrouve donc la relation hlg = (hg - hl) = T (sg - sl) = T slg.
L est une fonction décroissante de la température, nulle pour T supérieure à la température critique. Une formule due à Clapeyron permet d'estimer L à partir de la loi de pression saturante :
L = T (vg- vl) dPs/dT
Dans cette formule, le volume massique du gaz vg est obtenu à partir de l'équation d'état de la vapeur, et le volume massique du liquide vl à partir d'une relation appropriée.
Dans Thermoptim, nous avons retenu une relation donnant directement L en fonction de la température réduite Tr = T/Tc :
Calcul des propriétés d'un corps pur à l'état diphasique
Par application de la loi du mélange des phases, on a :
v = (1 - x) vl + x vg
u = (1 - x) ul + x ug
h = (1 - x) hl + x hg = hl + x L
s = (1 - x) sl + x sg = sl + x L/T
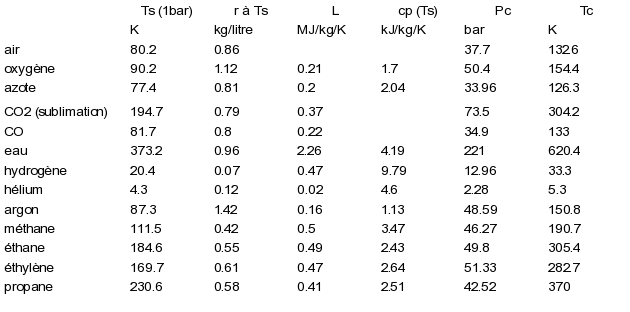
On trouvera dans le tableau ci-dessous les valeurs des coordonnées critiques et des chaleurs latentes de vaporisation pour quelques corps.
Caractérisation de l'état d'un fluide pur
Un fluide peut être présent sous une ou plusieurs phases.
S'il est monophasique et que l'on considère une petite particule de fluide, son état peut être défini par deux grandeurs comme sa pression P, sa température T, son volume massique v, ou encore son énergie interne massique u ou son enthalpie massique h, ou bien son entropie s.
Attention à ce que les pressions sont généralement exprimées en bar et non en Pascal, et les températures par défaut en Kelvin et en °C sinon.
A l'équilibre liquide-vapeur, lorsque le fluide est diphasique, la pression et la température ne sont plus indépendantes.
L'état de la petite particule de fluide peut alors être défini par une grandeur comme sa pression P ou sa température T, ainsi que :
soit son titre en vapeur x introduit précédemment
soit son volume massique v, ou bien son énergie interne massique u,son enthalpie massique h ou son entropie s.