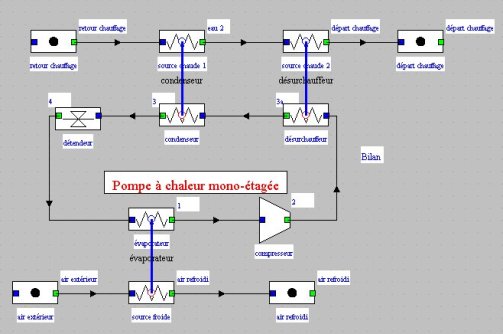
La modélisation dans Thermoptim d'une telle machine ne pose pas de problème particulier : il s'agit d'une variante du cycle de réfrigération simple.

Une fois que l'on dispose d'un modèle de pompe à chaleur réalisé dans Thermoptim (cf. figure ci-dessous), l'une des difficultés est de savoir comment le reparamétrer quand la température extérieure varie.

De nombreuses questions se posent en effet :

• comment évoluent les pressions d'évaporation et de condensation au cours du temps ;

• comment varie le débit du fluide thermodynamique ;

• quelle loi suit le rendement isentropique du compresseur ;

• quel pincement^[1] faut-il considérer dans les échangeurs ?

Ce n'est qu'en répondant de manière vraisemblable à ces questions que l'on peut espérer obtenir des résultats réalistes en terme de performances globales, notamment puissance de chauffage et COefficient de Performance de la machine.

Si l'on désire obtenir des réponses rigoureuses à ces questions, on est amené à effectuer ce que nous avons appelé dans ce portail des études de dimensionnement technologique et de simulation en régime non nominal, qui sont malheureusement très complexes et dépassent de loin ce qu'il est possible de faire dans le cadre de certains enseignements.

La solution que nous avons choisie consiste à se donner des lois empiriques "vraisemblables" pour un certain nombre de paramètres-clés, et de s'en servir pour reparamétrer le modèle de pompe à chaleur dont nous disposons.

Dans une pompe à chaleur, les deux types de composants qui jouent un rôle fondamental sont le compresseur (que nous supposerons volumétrique) et les échangeurs, notamment l'évaporateur et le condenseur, qui reçoivent l'essentiel des charges thermiques, le désurchauffeur dissipant une puissance plus faible.

Le compresseur

Comme indiqué dans la fiche thématique sur les compresseurs volumétriques, les paramètres-clés de ce type de composant sont son rendement volumétrique, qui représente la fraction de la cylindrée qui est effectivement utilisée, et son rendement isentropique, caractéristique des irréversibilités qui prennent place lors de la compression.

La figure ci-dessus montre l'allure de ces deux grandeurs et de leur rapport en fonction du rapport de compression, c'est-à-dire le rapport de la pression de condensation à la pression d'évaporation.

Le rendement volumétrique est une fonction linéaire décroissante, tandis que le rendement isentropique présente un maximum pour un rapport de compression fixé.

Nous pourrons donc nous donner deux lois pour représenter leur évolution dans le temps, à condition de connaître le rapport de compression.

Pression d'évaporation

La pression d'évaporation du cycle est déterminée par l'équilibre thermique de l'évaporateur, qui extrait de la chaleur de l'air ambiant. Elle est telle que la température de saturation du fluide frigorigène soit inférieure à la température extérieure, d'une valeur que nous appellerons pincement froid, et que nous déterminerons plus loin, dans la section traitant des échangeurs.

Pression de condensation

La pression de condensation du cycle est déterminée par l'équilibre thermique du condenseur, qui transmet sa puissance thermique au circuit de chauffage. Elle est telle que la température de saturation du fluide frigorigène soit supérieure à la température du circuit de chauffage, d'une valeur que nous appellerons pincement chaud, et que nous déterminerons plus loin, dans la section traitant des échangeurs.

Température du circuit de chauffage

Pour pouvoir chauffer des locaux, on utilise un circuit de chauffage composé d'éléments chauffants (les "radiateurs") qui fournissent une puissance thermique variable en fonction de la température extérieure, pour compenser les pertes thermiques du logement qui en dépendent directement. On peut en première approximation considérer pour cela que la température de départ du circuit de chauffage est fonction linéaire de la température extérieure.

Récapitulation provisoire

Compte tenu de ce qui vient d'être dit, et en supposant pour le moment connues les valeurs, en fonction de la température extérieure Text, des pincements chauds et froids Pinct_c et Pinct_f, nous pouvons opérer comme suit :

• la température de chauffage Tchauff est fonction affine de Text : Tchauff = a Text + b ;

• la pression de condensation est donnée par la loi de pression saturante du fluide : Pcond = Tsat(Tchauff + Pinct_c)  ;

• la pression d'évaporation est donnée par la loi de pression saturante du fluide : Pevap = Tsat(Text - Pinct_f)  ;

• le rapport de compression RC est donné par : RC = Pcond/Pevap ;

• le rendement volumétrique eta_v est donné par : eta_v = a RC + b ;

• le rendement isentropique eta_c est donné par une loi plus complexe, en pratique du second degré en fonction de 1/RC : eta_c = a + b/RC + c/RC/RC.

Débit de frigorigène

Le débit m_compr d'un compresseur volumétrique est fonction de nombreux paramètres, mais peut in fine s'exprimer comme proportionnel au rendement volumétrique eta_v et inversement proportionnel au volume massique du fluide à l'aspiration V1 : m_compr = K eta_v/V1.

Echangeurs de chaleur

Le comportement en régime non-nominal d'échangeurs de chaleur comme l'évaporateur ou le condenseur-désurchauffeur est assez complexe à modéliser, aussi n'essaierons-nous pas de le faire de manière détaillée. Nous nous contenterons de partir du bilan thermique global de l'échangeur, qui exprime que la puissance thermique P transmise est proportionnelle à l'écart de température entre les deux fluides Delta T et au produit de la surface d'échange A par le coefficient d'échange thermique global U : P = UA Delta T.

U varie en fonction de Text et de m_compr, mais peu, et nous pouvons en première approximation le considérer constant. A est bien sûr constant, et cette équation se réécrit sous la forme : Delta T = P/UA.

Dans le condenseur et l'évaporateur, d'une part la température du fluide frigorigène reste constante, et d'autre part les débits de l'air et du fluide de chauffage (de l'eau) sont importants, de telle sorte que leur température varie peu. Delta T représente donc le pincement chaud ou froid selon le cas.

Sa valeur dépend donc de la puissance thermique échangée, de telle sorte que cette équation introduit un couplage entre les hypothèses et les résultats. Nous pouvons simplifier les choses en considérant que la puissance thermique est une fonction croissante de la température extérieure, et en faisant l'hypothèse que les deux pincements sont des fonctions affines de Text.

Les deux dernières équations de notre modèle deviennent :

Pinct_c = a Text + b ;

Pinct_f = a Text + b.

Conclusion

Nous avons ainsi mis en évidence neuf équations permettant de calculer les paramètres du modèle de pompe à chaleur en fonction de la température extérieure. Il suffit pour pouvoir exploiter le modèle de créer un pilote dont la seule entrée est Text, qui vient ensuite mettre à jour tous les paramètres et recalculer le cycle.

Bien évidemment, les valeurs des coefficients a, b, et c diffèrent d'une équation à l'autre et doivent être judicieusement choisis.

Pour éviter des problèmes de convergence dans le calcul, et notamment des inversions de température au niveau des échangeurs de chaleur, les modifications des paramètres sont effectuées de manière progressive.

La classe externe PilotePAC_f_Text.java, dont le code dans la liste des pilotes est "PAC f(Text)", permet d'effectuer ces reparamétrages.

Elle a de plus été écrite pour pouvoir être émulée à partir d'un client externe dans le cadre d'un fonctionnement de Thermoptim en réseau.

Vous trouverez ci-dessous une archive contenant les fichiers permettant de faire fonctionner ce modèle. Attention : ce nouveau pilote nécessite une version de extThopt2.zip postérieure au 28/09/2012. Si nécessaire, faites la mise à jour avec le fichier fourni.