Presentation of the exercise
In their article B1 250 from the Techniques de l’Ingénieur, titled “Production d’énergie électrique à partir des combustibles fossiles”, whose summary can be downloaded through one of the links below, MM. Bolard et Metz present a 300 MW steam power plant, whose capacity corresponds to that most frequently used in the world.
The objective of the exercise is to model such a power plant in Thermoptim in order to assess its main characteristics.
This exercise is comprised of three parts :
- in the first part (session S26En), we suppose that the plant uses a single circuit.
- in the second part (this one), we take into account an extraction and a reheat which occur in industrial machines. The model becomes much more realistic.
- in the third part (session S28En), we quantitatively analyse the irreversibilities of both cycles through their exergy balances.
Comparison with Carnot cycle

Steam power plants

- Carnot Comparison
- (1-a-d-e) or (1-b-3-4) impossible (too high pressures)
- (f-c-d-e) technologically impossible (two-phase expansion)
Basic cycle improvements
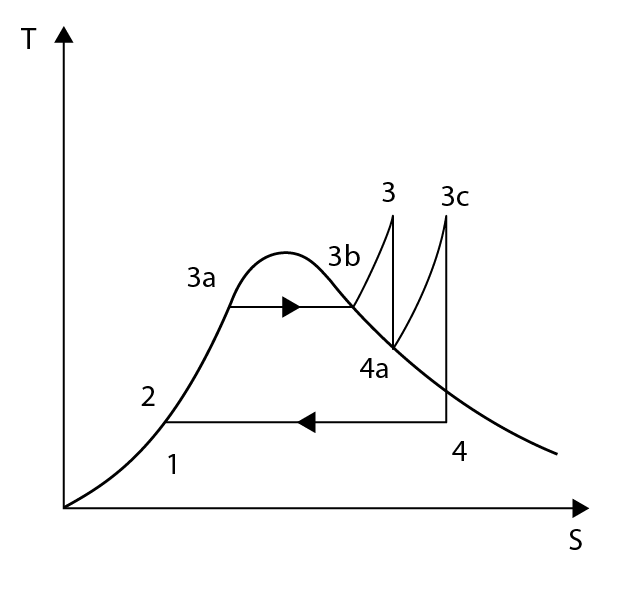
- Reheat
- para-isothermal
Basic cycle improvements

- Extraction
- Partial regeneration
- Only if exhaust gas tempereture is high
- (not for combined cycles)
Steam power plants


Extraction and reheat cycle

Extraction and reheat cycle

Setting the model
When the simulator elements are created, Thermoptim initializes all the points with a pressure of 1 bar and a temperature of 300 K, which must then be modified according to the data of the problem you are studying.
The two steps that follow will show you how to set points and processes, then the next will remind you of the values that you should enter in Thermoptim.
Extraction and reheat cycle

Setting the parameters of points and processes
Set now the parameters of the various points one by one, checking that you enter the values of the temperature known (4a), as well as those of the pressures(points 4a, 3c, 2, A and B), as Thermoptim does not set them automatically. In order to do that, follow these steps:
- open point point 4a, enter a pressure of 15 bar and click on “Calculate”
- then open point 2, enter a pressure of 15 bar, and click on “Calculate”
- open point 3c and enter a pressure of 15 bar, and a temperature of 542 °C, then click on “Calculate”
- open point A, enter a pressure of 15 bar, and click on “Calculate”
- open point B and enter a pressure of 169 bar, and calculate it
Set then the process’s parameters, for which default options are valid: the new compression and the expansion are adiabatic, calculated with the isentropic reference, and their isentropic efficiencies are known. In order to do that, follow these steps:
- open process “HP turbine”, enter a flow-rate of 215 kg/s then click on “Calculate”, which provides point 4a temperature (230 °C)
- recalculate the divider to update its branches
- open process “reheat”, change its energy type as “purchased” and click on “Calculate”. The temperatures of their inlet and outlet points being known, its enthalpy can be calculated
- open process “LP turbine”, and enter an isentropic efficiency of 0.85, then click on “Calculate”, which shows that point 4 is at the saturation temperature (29 °C), is quality being equal to 0.979
- calculate the mixer which determines point A temperature (127.3 °C)
- open process “feedwater pump”, whose isentropic efficiency is by default equal to 1, then click on “Calculate”, which sets the temperature of point B (128.65 °C)
Recalculate the project several times from the simulator screen, so that all processes are updated.
Extraction and reheat cycle

Summary
This exercise has allowed you to study a simple steam cycle and to learn how to model it in Thermoptim. This is but a simplification (cycle without reheat nor extraction) of a 300 MW power plant of the type described in the article B1 250 of the Techniques de l’Ingénieur.
The new model is more complicated than the previous one: it introduces an extraction at medium pressure and involves a divider and a mixer.
We chose a setting that seemed realistic, but that is not the only one possible, especially because the new configuration adds two degrees of freedom to the model: the pressure level and the extraction flow rate.
As an exercise, you can perform a sensitivity study on the influence of these two parameters on the performance of the cycle.
You will thus show that there is an upper limit to the extraction rate, which corresponds to the case where the water at point A is biphasic. Thermoptim then refuses to calculate the second compression.