Thermodynamics of heat exchangers
This session discusses the thermodynamics of heat exchangers, and explains how to build them in Thermoptim.
The calculations are based on the NTU method, which gives access to the product UA of the overall heat exchange coefficient by the exchanger surface.
In Thermoptim phenomenological version, it is not possible to calculate U, due to the absence of a detailed geometrical description of the exchanger.
This approach, however, already allows for sizing heat exchangers that are involved in many energy systems.
Professional and industrial versions of Thermoptim include a powerful optimization method, derived from the pinch method, which enables the design of complex networks of heat exchangers.
Course reference:
- Volume 1, Chapter 5
To follow the presentation, go to next step
(Session realized on 06/16/11 by Renaud Gicquel)HEAT EXCHANGERS
- Heat transfer between two fluids
- Flow arrangements
- counter-flow, most efficient
- parallel-flow
- cross-flow
HEAT EXCHANGERS
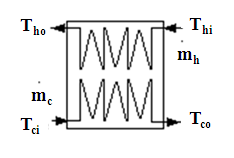
index h : hot fluid
index c : cold fluid
index i : fluid inlet
index o : outlet
Tci : cold fluid inlet temperature
m dot : flow rate
HEAT EXCHANGERS
- Heat flux exchanged
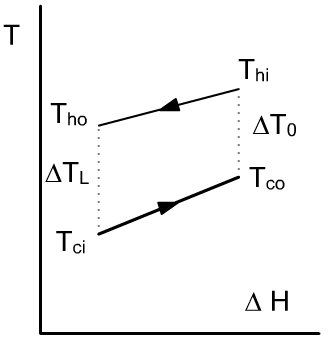
HEAT EXCHANGERS
-
Number of Transfer Units method
HEAT EXCHANGERS
- Method of the Number of Transfer Units
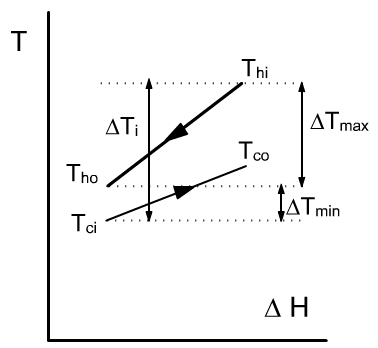
HEAT EXCHANGERS
- ε = f(NTU, R, flow pattern)
- Counter-flow heat exchanger
HEAT EXCHANGERS
- Heat exchanger pinch
- minimum temperature difference between both fluids
- most constrained zone of the system
HEAT EXCHANGERS
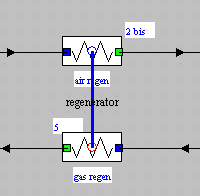
- Heat exchanger in Thermoptim
- Connects a hot stream and a cold stream
- Two “exchange” processes already calculated (ΔH ≠ 0)
HEAT EXCHANGE

HEAT EXCHANGERS

- Heat exchanger in Thermoptim
- Connect the two exchanger connection ports of the “exchange” processes
- Click twice on the blue link
HEAT EXCHANGERS
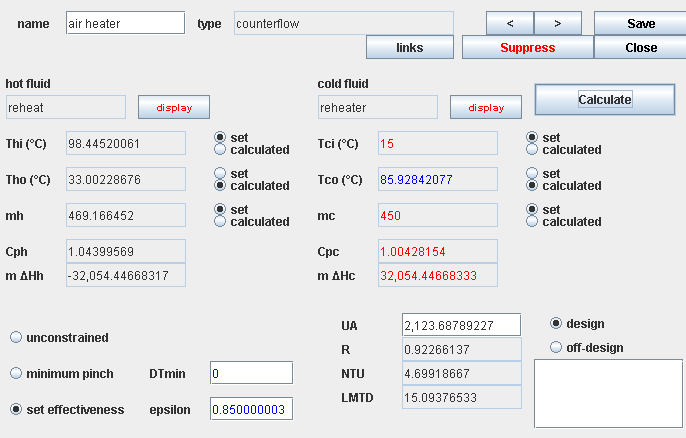
HEAT EXCHANGERS
- Six variables (Tci, Tco, mc, Thi, Tho, mh)
- Enthalpy conservation
- Five degrees of freedom
- One flow rate at least must be set
- If vaporization plateau, ΔT = 0.1 K
- It may be necessary to calculate several times
SETTINGS
- generally, Tci, mc, Thi, mh known
- In addition, we set:
- Either an outlet temperature (steam generator of a steam power plant)
- Or an effectiveness (GT regenerator)
- Or a pinch value
- Rarely, the 4 temperatures and a flow-rate are known, and we seek the second flow-rate
- other settings in exceptional circumstances
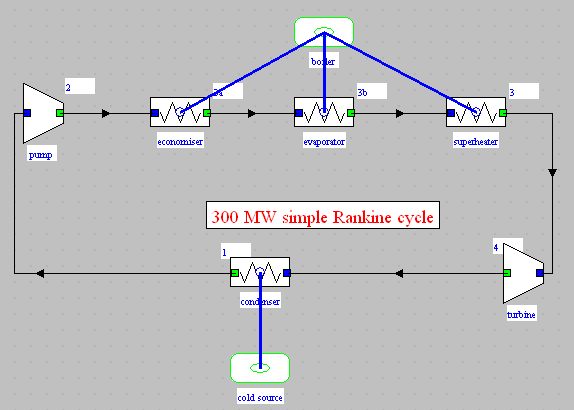
Steam cycle diagram
Boilers

- radiative protection of the tubes
- approach subcooling
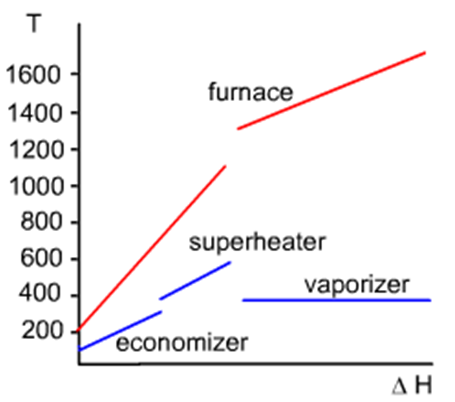
Steam power plant with boiler
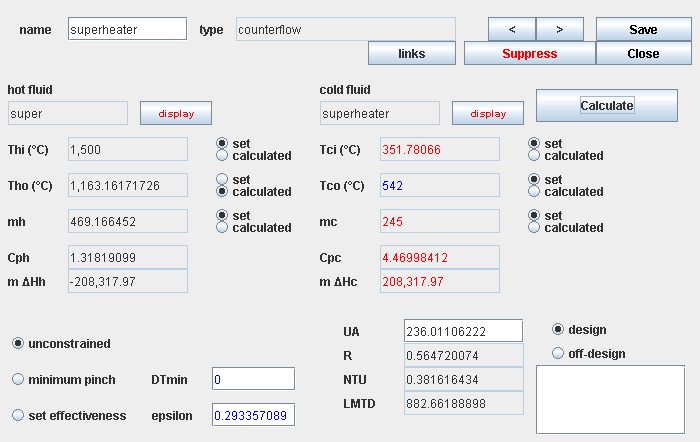
Superheater
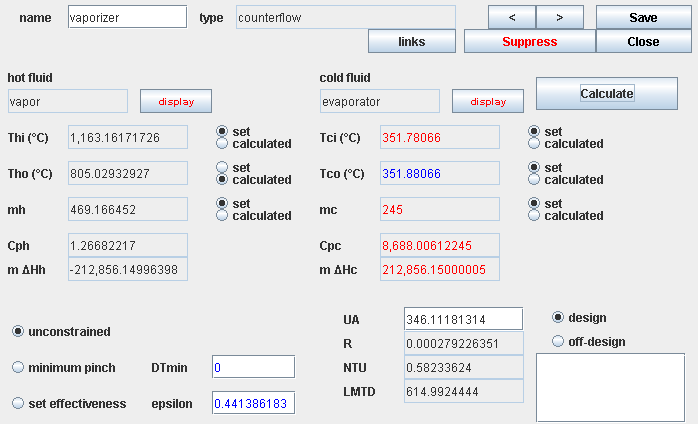
Vaporizer
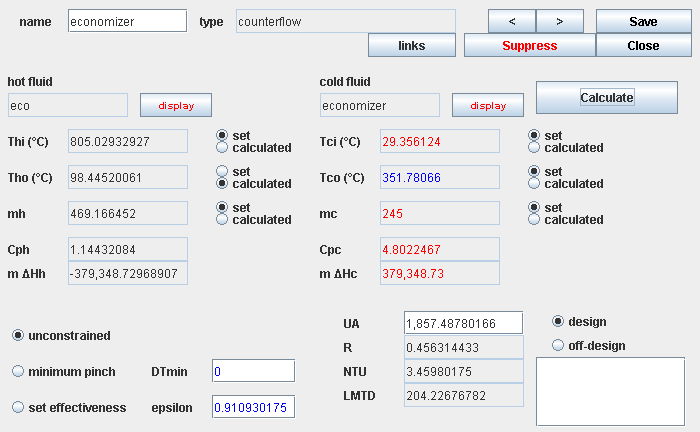
Economizer
Air heater

Thermodynamics of heat exchangers
This session discusses the thermodynamics of heat exchangers, and explains how to build them in Thermoptim.
It showed the following:
- a heat exchanger connects two exchange processes, the “hot” one, which cools and the “cold” one, which heats up
- calculations are based on the NTU method, which only gives access to the UA product of the heat exchanger
- thermophysical properties of both fluids being assumed to be constant in this method, small differences exist in relation to Thermoptim calculations, more accurate
Setting heat exchangers
For temperatures, we can set explicit constraints (e.g. set inlet fluid temperature), or implicit constraints (we set the exchanger effectiveness value, or the pinch minimum value).
For the problem to have a solution, we must set a total of five constraints, among which one set flow. If one of them is implicit (set pinch or effectiveness), four explicit must be (3 temperatures and a set flow, or 2 temperatures and 2 set flows). Otherwise five must be set.
Examples of construction of heat exchangers
In addition to the one built in this session, three exercises show you how to construct heat exchangers (the links below give you direct access to them):
- in session S41En three exchangers in series form the heat recovery steam generator (HRSG) of a single pressure combined cycle. We have here to determine the outlet temperatures of gases in the HRSG, the other variables being known
- in session S23En, we must set a gas turbine regenerator of given effectiveness
- in session S33En a heat pump evaporator is constructed and sized, that is to say that its exchange area A is calculated (whereas Thermoptim gives only access to UA).
