Adiabatic compression and expansion
This session discusses the thermodynamics of adiabatic compressions and expansions.
Much of the presentation being valid for both types of processes, we first deal with compression, the specifics relating to expansion being given at the end.
As the components in which these processes take place are assumed adiabatic (that is usually the case in real machines), their heat exchange with the surroundings is zero.
It follows that the reference process is reversible adiabatic, also called isentropic.
Moreover, at the entrance and exit of these components, the velocities of fluids are always relatively low, so that the kinetic energies are negligible.
Under these conditions the first principle writes simply for heat exchangers: Δh = τ
Calculate the heat brought into play in these components is to determine the enthalpy change of the fluid flowing through them.
Course reference:
- “Technological Components / Compression”
- “Technological Components / Expansion (with work)”
To follow the presentation, go to next step.
(Session realized on 06/16/11 by Renaud Gicquel)COMPRESSION / EXPANSION
- work put in play τ = Ta f(Pr/ Pa)
- increasing function of compression ratio Pr/ Pa
COMPRESSION / EXPANSION
- work put in play τ = Ta f(Pr/ Pa)
- increasing function of compression ratio Pr/ Pa
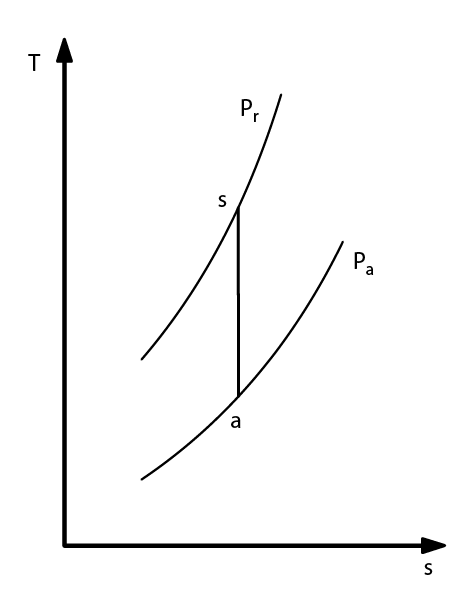
- Ideal process:
- isentrope τs
COMPRESSION THERMODYNAMICS
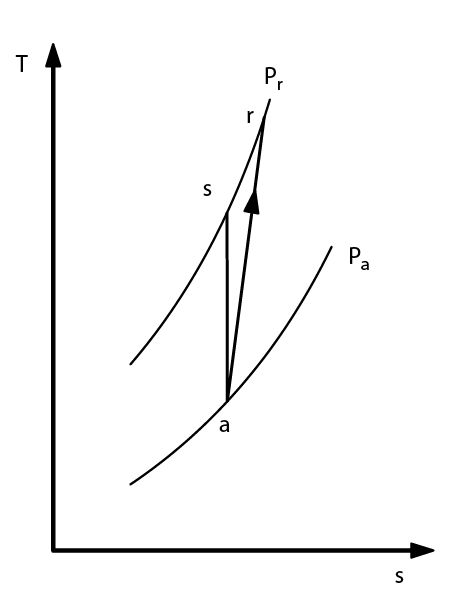
- Real adiabatic compression
COMPRESSION THERMODYNAMICS
- Real adiabatic compression
- ηs isentropic or adiabatic efficiency
- determined experimentally
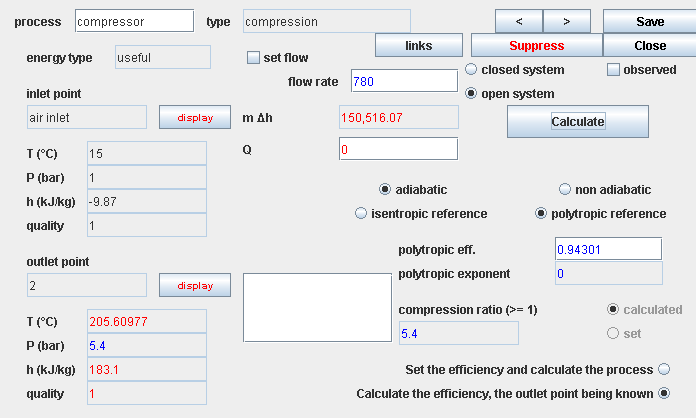
Compression calculation steps
- calculate the entropy at suction: s(Pa, Ta)
- reverse in Ts: s(Pr, Ts) = s(Pa, Ta)
- calculate: Δhs = h(Pr, Ts) - h(Pa, Ta)
- calculate: hr = h(Pa, Ta) + Δhs/η
- reverse in Tr: h(Pr, Tr) = hr
COMPRESSION THERMODYNAMICS
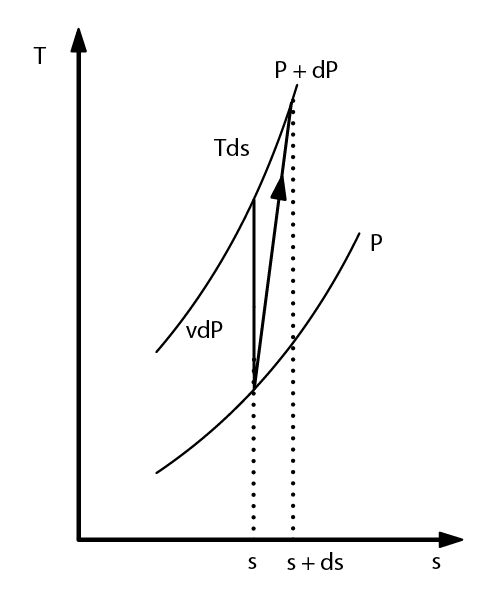
- Reversible adiabatic compression work
- (4.1.5)
- (4.1.6)
COMPRESSION THERMODYNAMICS
COMPRESSION THERMODYNAMICS
- polytropic
- k polytropic coefficient or exponent
-
(4.1.9)
COMPRESSION THERMODYNAMICS
- Compression ratio in a compressor stage always limited
- Dynamic compressors (4.1.26)
- Displacement compressors
- (losses, dead space)
- Staged compressions
Isentropic efficiency versus compression ratio
It is important to keep in mind that the isentropic efficiency of a compressor depends on the compression ratio, whatever the technology used.
For a displacement compressor, the law giving its value must be determined experimentally.
For a multi-stage dynamic compressor, it can be estimated if one knows the polytropic efficiency.
The underlying assumption in the polytropic approach is indeed that irreversibilities are uniformly distributed throughout the compression.
This hypothesis is well respected in the multi-stage dynamic compressor all stages of which have the same compression isentropic efficiency.
The isentropic efficiency of this stage can then be regarded as the polytropic efficiency.
This important issue is discussed thoroughly in the textbook.
COMPRESSION THERMODYNAMICS
- Stage compression ratio (4.1.27)
- Intermediate cooling if possible
COMPRESSION EXPANSION 
EXPANSION THERMODYNAMICS

- Real adiabatic expansion
EXPANSION THERMODYNAMICS
- polytropic
- (4.1.27)
Compressions and expansions
This session discusses the thermodynamics of compressions and expansions.
We have shown that:
- the reference compression or expansion is usually isentropic
- taking into account the irreversibilities can be done either by an isentropic efficiency, or by a polytropic efficiency (valid for Turbomachinery)
- compression or expansion is usually multistage